【医療統計YouTube】95%信頼区間【第8回】
今回もまたなかなか時間を要してしまいましたが、新しいyoutube動画公開しました。
今回のテーマは95%信頼区間です。
その意味がどうしても取りづらい概念で、統計学の歴史に詳しい『統計学を拓いた異才たち』を見ても、初めて学会発表された際の混乱した様子がうかがえます。
この本では1934年に区間推定の生みの親であるイェジー・ネイマンが発表したときのA.L.Bowleyという統計学者の反応が書かれています。
「これは、われわれが必要とすることーサンプリングにおける母集団に対して、その信頼区間が一定の範囲内に収まる可能性ーを示してくれるのだろうか。そうではないのだろうか、いや、私は自分の考えを適切に表現できているのかどうかさえも、よくわからない。しかし、この方法が初めて示された時から、どうも問題があるように思えてならない。この理論の展開は説得力がないので、自分が納得できるまで信頼区間の妥当性を疑わざるを得ない。」(『統計学を拓いた異才たち』第12章「信用」詐欺より引用)
うーん、何を示すものなのかよくわからない気持ちになっていたわけですね。実際のところ、この区間推定は”一定の範囲内に収まる可能性”を示す指標ではないので、名前に反していて理解しにくいのかと思います。
ここで数式が理解できると本質的な意味がもう少し分かりやすくなり、動画で紹介していたような仮説検定と対応した概念ということもよくわかります。以下に一度式の流れを書いてみますので、細かい数式はわからない人でも気にせずに雰囲気だけみてもらえるとよいかもしれません。
数式的な補足
例として中心極限定理を用いて正規分布に近似できるようなサンプル数を集めた標本平均があったとします。
この標本平均は平均と分散
(母分散は
)に従う正規分布となります。
ここで
対立仮説
であるとして、有意水準5%の統計学的仮説検定を行います。つまり母平均がであるという仮説を検定するわけです。
すると受容域、つまり母平均がであることを正しいとする場合は
と示されます。
ここで母平均を不等号の中心にして式を変形すると以下のようになります。
つまり信頼区間の算出はもともとの仮説検定の式を変形しただけなんですね。数学的には全くの同値であることがわかります。こうみると標本平均±1.96標準誤差を示す式になっていることも理解できます。
さらに細かいことを言えばこの標本平均は実現値ではなく変数です。統計学では小文字で実現値を書くことになっていますので(
という感じ)実現値を代入したら、この不等式を満たすか満たさないかはひとつに決まります。つまり、動画で述べていたように、この式があらわすことは母平均がこの範囲をとる確率が95%ではないということですね。
なお、今回は分散が既知としていますが、実際は未知のことが多いのでここも推定値を用いて計算することになります。
ちなみに、真の値を含む確率が95%と区間というものも実はありまして、ベイズ信用区間(Bayesian credible interval)と言われています。ベイズ統計では「母平均は固定されたもの」とは考えず、確率分布に従うものとみなすため、真の値を含む確率が95%となるような区間を求めることができます。
ベイズの法則に出てくる事前確率・事後確率と同様に事前分布・事後分布という確率の分布を想定するため、事前分布に何を用意するかによって変化しますから、ここで出てくる95%信頼区間とは基本的に異なる数値となります。
参考文献:
Judea Pearlの入門統計学的因果推論を読んでみよう③
第3章の内容に入っていきたいと思います。
介入についてです。ここからが重要かつ複雑になってきます。
前回までの記事はこちら
Judea Pearlの入門統計学的因果推論を読んでみよう①
Judea Pearlの入門統計学的因果推論を読んでみよう②
目次:
介入と条件付けの違い
さて、医学の臨床研究で知りたいことというのは多くの場合、ある介入を行うとどうなるかという点です。例えばある薬を飲むと、ある病気が治る確率が上がるのかどうか、ということでしょう。
それがわかるための最も確実な方法は質の良いランダム化比較試験ですが、費用や症例数の観点から難しい場合も多くみられます。そこで観察研究などが代わりとなれば良いわけですが、観察研究において薬を飲む飲まないを分けて評価した場合、さまざまなバイアスが入り込みます。
例えば、重症な人は薬を飲む確率が高いが、その分病気も治癒しにくいため、本当は有効であるが治る確率は低く見える。
DAGにするとこのような感じでしょうか。

そうした場合、重症度に応じて条件付けすることで疑似的に内服群・非内服群を同等とし、比較するという方法が考えられます。
ではこの時に、条件付けするべき因子はどういったものを選ぶべきなのでしょうか?そしてその因子で補正した効果が介入と同等と言える理論の背景は何なのでしょうか?
それを求めていくのが第3章の内容となります。
まず最初は
・観察研究において「薬を飲む人に限って条件付けした場合」
・ランダム化比較試験において「薬を飲む人と飲まない人を振り分けた場合」
ではそれぞれ疾患の治癒する確率が異なる、ということに着目します。
それぞれどう違うのか、どうすれば一致するのかを次に掘り下げていきます。
doオペレータを用いた修正後確率
ランダム化比較試験のような介入を行なった場合の確率と上記のような条件付けを行なった確率というのは基本的に異なります。
具体例として、先程のような病気の重症度、薬の内服(ありをX=1、なしをX=0)、病気の治癒(治った場合をY=1、治らなかった場合をY=0)の3つを取ったDAGで考えてみましょう。
この場合、観察研究における「薬を飲む人」というのは「より重症である」人たちになります。母集団が重症者にやや偏るわけです。
ところがランダム化比較試験のような強制的な介入を行う場合、疾患のある人たち全体が母集団となります。重症な人も軽症な人も全て一様に薬を内服するという介入をされるため、母集団は全ての人です。それぞれ母集団が異なるため治癒する確率も異なるものとなります。また、強制的な介入によってDAGも修正され、以下のような形となります。

この場合の確率はdoオペレータという表記を使って
と表され、通常の条件付き確率とは区別されます。
これに対して、ただ薬の内服の有無で条件付けされた場合に母集団となるのは実際に内服をした人たち、あるいはしなかった人たちとなります。例えば重症な人の方が内服しやすいのであれば、内服した人たちは重症者にやや偏った母集団なわけです。そのため先程の確率とは分布が異なると考えられます。
この場合の確率は単純に
と表されます。
平均因果効果と調整化公式
ここで我々が知りたいのは最初に述べたように介入の有無による効果の違いを知りたいわけです。これは平均因果効果(ACE: average causal effect)と呼ばれ、式としては
となります。
というわけでこのdoオペレータを使った式を求めていきたいわけですが、どうすれば良いのか。そこで登場するのが調整化公式です。
まず記号としてdoオペレータを使った式は上述のようにDAGそのものが変化してしまうわけでした。そこでそれを修正後確率として以下のように区別して用いることとします。
この時、実は
となることがわかります。
これは以下の2つの状況を考えるとわかります。
①ZとXの両方で条件付けした場合の疾患の治癒率は変化しません。例えば、重症者かつ内服した場合に病気が治癒するかどうかということは強制的に内服させるかどうかとは関連しないことを考えればわかります。
②内服を強制的にしようが、自然に任せようが、疾患が重症となる確率は当然変化しません。ZはXの子ではないためdoオペレータだろうがどうだろうが、Zの確率自体は変化しません。
よってこれらを用いると
となり、doオペレータを使った確率と観察可能な条件付き確率を等式で結ぶことができました。(和の記号は全てのzの値について足し合わせています)
なお、式変形の途中でわかりづらい点がいくつかありますが、2-3行目の変形は、3変数の条件付き確率の場合
となります。初項では両方の確率でXが条件付けされていないといけません。
また3-4行目の変形ではXとZが独立(前回紹介したd-分離)であることを用いています。条件付き確率では互いの変数が独立である場合
となります。
改めて先ほどの式の最初と最後を書き直しますと
となります。この式は調整化公式と呼ばれています。ここからそれぞれのXの値についての確率を計算すれば先程のACEを求めることができるわけです。
なお、一般化して考える場合、今回のZのようにXの親となる変数について調整すれば良いので、Xの親をPAとして
となります。
今回の例ではXの親について調整することで、観察データからdoオペレータを用いた修正後確率を計算することができましたが、Xの親が十分に観測できない場合も多数あると思われます。そこで実際どの変数について調整をすれば良いのか。それを求めるための基準がこれまた最近よく聞かれるバックドア基準となります。次回の記事で勉強していきます。
【効果、有効性】effect/ effectiveness/ efficacy/ utilityの違い【医学論文の英語表現】
今回は効果や有効性、有用性などの意味で使われる名詞を比較していきます。eff-から始まる単語は3つもありますが、少し意味が異なるため今回入れなかったものとしてefficiency(効率)なんかもあって、かなり紛らわしいです。
以前書いたinfluence, impactなども近い意味合いがあります。
目次:
単語の意味と共起表現
・effect
the result of a particular influence
まずは最もシンプルなのがこのeffectです。原義もこのようにシンプルでinfluenceによる結果とされています。
良い意味でも悪い意味でも染まるものだと思いますので、医学論文ではpreventive, beneficial のような形容詞を伴って使われることが多くみられました。
・effectiveness
the degree to which something is effective
how well a particular treatment or drug works when people are using it, as opposed to how well it worksunder carefully controlled scientific testing conditions:
さて続いてはeffectivenessですが、こちらはその効果についての「程度」の意味合いを含みます。また、実際に行ってどうであったか、という印象もあり、real world effectivenessやcost effectivenessといった例がみられます。
・efficacy
the ability, especially of a medicine or a method of achieving something, to produce the intended result
これは特に良い悪いの印象をもたないeffectと違ってintended resultとあるように、ある程度期待された効果が出ていて、その能力がどうなのか、ということを論じる際に使われています。日本語で「有効性」と訳されることがありますが、まさに有効であることがある程度前提になっているためと思われます。
・utillity
the usefulness of something, especially in a practical way
こちらは利便性という意味に近く、上記の用語と異なって薬剤以外に広く用いられやすい印象があります。通常の文章では同じ単語でインフラを示すこともありますね。
論文でよく見られたのはcost utility, clinical utilityといった表現でしょうか。検査や診察所見の有用性という意味ではこちらの方が適していそうです。
(Cambridge Dictionary | English Dictionary, Translations & Thesaurus
単語の原義はこちらから引用)
(SKELL)
医学論文を含めた用例
・effect
Effect of Aspirin on All-Cause Mortality in the Healthy Elderly
the progressive separation of the cumulative incidence curve for cancer-related death in the aspirin group from the curve in the placebo group are in favor of a true effect.
(doi: 10.1056/NEJMoa1803955)
アスピリンによる影響を調べた論文です。上述していたようにeffectは比較的中立的な表現かと思いますので、形容詞を伴って使われています。
この論文はアスピリンの一次予防の効果を調べたASPREE試験の論文で、明らかな有効性は示せていませんでした。そういう意味合いもあってefficacyではなくeffectなのかなと思ってます。
Beneficial effects of corticosteroids on ocular myasthenia gravis
(doi: 10.1001/archness.1996.00550080128020)
眼筋型MGのステロイドの効果を調べた論文ですが、こちらも観察研究なので、beneficialとはありますが、中立的なeffectが使われているのかと思います。
・effectiveness
The utility of removing autoantibodies in generalised myasthenia gravis has been demonstrated by the effectiveness of plasma exchange and immunoadsorption.
すでに実証された「有効性」ということでここはeffectivenessですね。
Meta-analysis and cost-effectiveness of second-line antiepileptic drugs for status epilepticus
(Neurology 2019 May 14;92(20):e2339-e2348.)
現実的な効果・有効性という意味ではeffectivenessが使われるということでcost-effectivenessという表現はよく見かけます。
Real-world effectiveness of ramelteon and suvorexant for delirium prevention in 948 patients with delirium risk factors
(Journal of Clinical Psychiatry, (2020), 81(1))
こちらも同様に実際の効果ということでreal-world effectivenessとなっています。
・efficacy
Evaluation of efficacy and tolerability of first-line therapies in NMOSD
Neurology, (2020), e1645-e1656, 94(15)
efficacyは第3相試験ではほぼ確実に認められる単語ですね。大抵の場合はevaluate, assessといった「評価」の単語と並べて使われます。
Evaluation of Aducanumab for Alzheimer Disease: Scientific Evidence and Regulatory Review Involving Efficacy, Safety, and Futility
(doi:10.1001/jama.2021.3854)
The phase 3 ADAPT study aimed to assess the safety and efficacy of efgartigimod, in patients with generalised myasthenia gravis.
(Lancet Neurol 2021; 20: 526–36)
efficacy and safetyは常にセットで見かけますね。
・utility
Our result of 71% sensitivity falls at theupper limit of this range and suggests increased utility of AChR antibody testing as a diagnostic tool.
(JAMA Neurology, (2015), 1170-1174, 72(10))
こちらは診断のための検査の有効性という意味で使われます。他にも上述のeffectivenessの例の一つ目にもutilityは使われていますね。
・impact(おまけ)
効果とも訳せる言葉ですが、ネガティブあるいはポジティブな価値判断が含まれていたり、何か目新しく影響が大きい場合に使われているようです。
Potential impact of missing outcome data on treatment effects in systematic reviews: imputation study
No methodological study has yet assessed the impact of different assumptions about missing data on the robustness of the pooled relative effect in a large representative sample of published systematic reviews of pairwaise comparisons.
(BMJ (Clinical research ed.), (2020), m2898, 370)
欠損データがいかに研究結果に影響を与えているかを示した論文でその影響の大きさやネガティブさを強調する意味合いでimpactなのだろうと思っています。
Our study adds to understanding the crucial role of SDOH in impacting health outcomes.
Stroke, (2020), 2445-2453, 51(8)
(SDOH; Social determinants of health)
こちらも同様に全般的に与える影響の大きさを持ってimpactという動詞が用いられています。
*1:Lancet Neurol 2021; 20: 526–36
Judea Pearlの入門統計学的因果推論を読んでみよう②
引き続きまして『入門統計学的因果推論』の第2章を読み進めてみます。ここからは具体的なグラフィカルモデルの応用になってきます。
目次:
条件付き独立と条件付き従属について考える意義
ここからは前回説明したSCMおよびグラフィカルモデルにおいて各変数が条件付き独立なのか従属なのかをどのようにして考えるか説明していきます。
その前になぜ、条件付き独立や従属が大事なのか。
本書の冒頭でも触れられているようにいわゆる「シンプソンのパラドックス」において、全体をみるか、層別化してみるかを考えたいとき、この考え方が必要になってきます。
観察研究において何らかの介入の効果を考えたいときは交絡因子の影響を取り除きたいのが通常です。
例えば、ある薬を内服するかどうかが、ある病気を治癒するのに役立つかどうかを考えてみます。健康的な生活習慣で真面目な人は、薬の内服もしやすいし、病気も治癒しやすいとしてみましょう。グラフィカルモデル風に考えると以下のようになります。
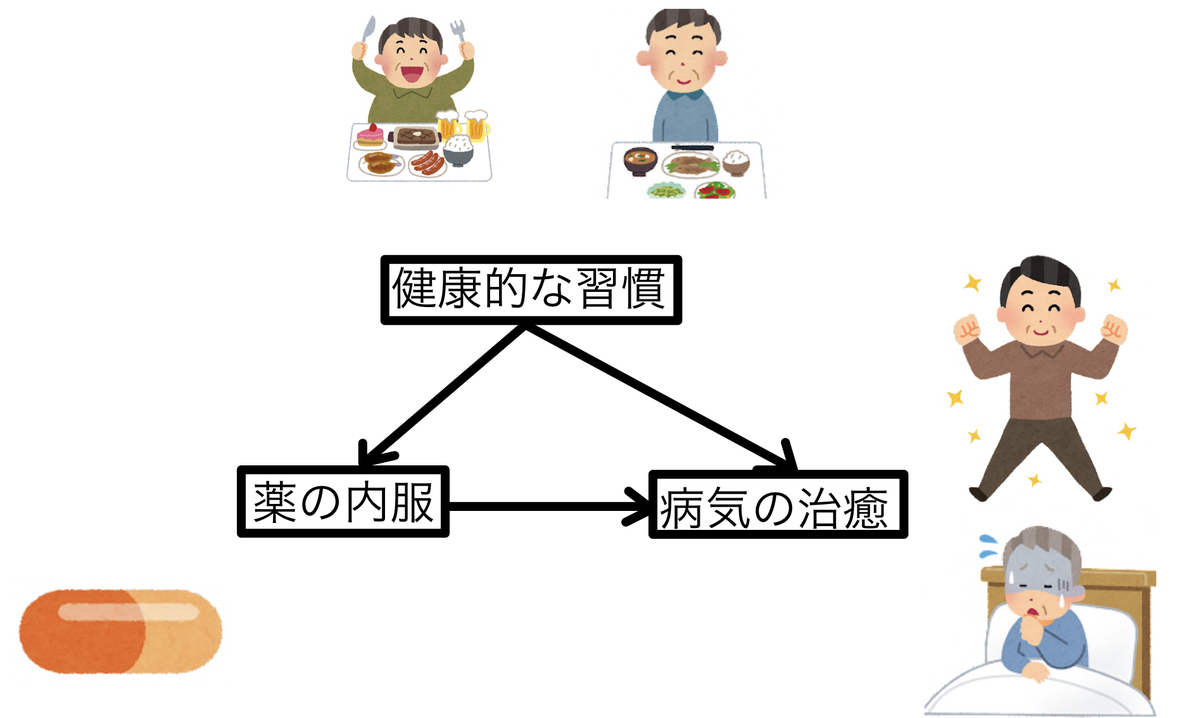
この時、薬の効果を純粋に考えるには交絡因子である「健康的な生活習慣」の影響を取り除かなければいけません。単純に薬の内服あり・なしで結果を出すと内服のある人は健康的な生活習慣をしている可能性が高いため、病気の治癒の効果もさらに上乗せされて見えてしまうからです。
つまり、「薬の内服」と「健康的な生活習慣」を独立の関係にしなければいけないわけです。
そのための答えは「健康的な生活習慣をしているかどうかで層別化する(条件付け)」ことになります。こうすることで初めて純粋な薬の効果を推定することができます。
よって、どれを条件付けするとどの変数が従属あるいうは独立になるのか、ということが重要になります。グラフィカルモデルの形によってその規則性は色々とあり、今回順番に確認していきます。また従属・独立の定義はそもそも何なのかも改めて見ていきます。
独立と従属の式における定義
SCMにおいては独立・従属あるいは条件付き独立・従属ということを式で表すことができます。これがグラフィカルモデルでは見ただけでわかるようになっていますので、利点の一つとなっています。
まずSCMにおける独立・従属がどのように表されるかみていきます。
SCMで“変数XとYが独立である“とは次のような定義が当てはまります。
つまり、Yがどのような数で条件付けされようが、Xがとる値の確率にはなんら影響を及ぼさないということですね。
逆に、“XとYが従属である”場合は
となるようなyが存在する、ということになります。
また、あるもう一つの変数の条件付けの下で、二つの変数が独立あるいは従属になる場合があります。“Zの条件付けの下でXとYが独立である”という場合は
と表すことができます。
では、どのようなグラフィカルモデルだと従属・独立あるいは条件付き従属・独立になるのか。そのパターンをそれぞれ見ていきます。
連鎖経路(chain)

まず連鎖経路(chain)と呼ばれるのはこのように連なった形をしているものを指します。この時、XとYとZはそれぞれ有向道で繋がっており従属の関係にあるのはすぐ分かりますが、大事なのは条件付きにした時どうなるか、ということです。
結論から述べれば、連鎖経路ではXとZの間にあるYが条件付けされると独立となります。
例えば、親の年収(X)がどの大学へ行くか(Y)に影響し、どの大学に行くか(Y)がどの企業に就職するか(Z)に影響すると仮定してグラフィカルモデルを書くとしましょう。親の年収(X)はどの企業に就職するか(Z)には直接影響しないという前提です。
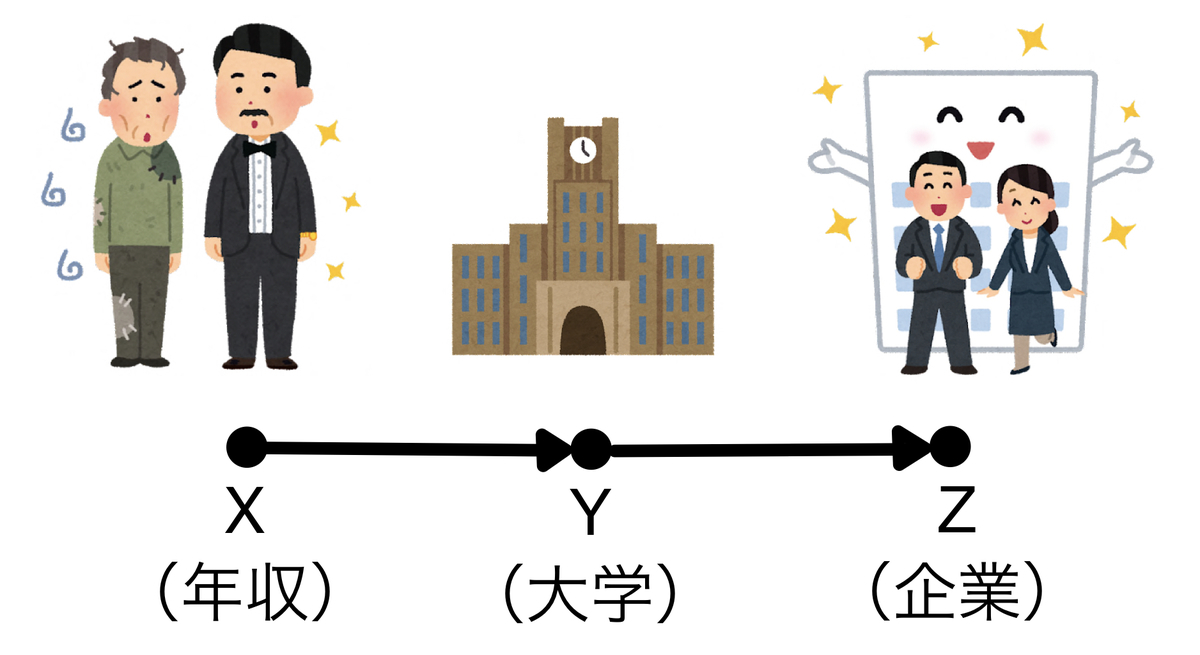
そうすると、どの大学に行くかを固定すれば(条件付け)どの企業に就職するかは自ずと決まってきます。つまり、親の年収(X)と就職先の企業(Z)が独立となるわけですね。
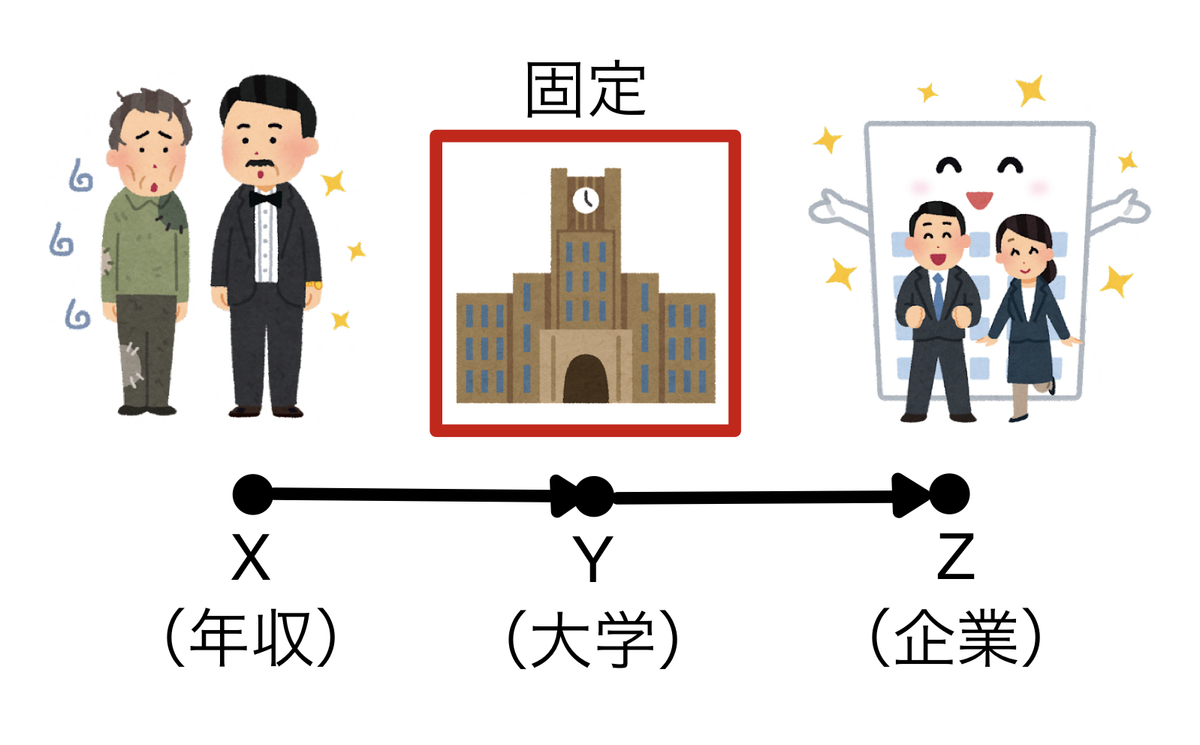
これと同様にグラフィカルモデルの形によって、どうしたら条件付き独立・従属となるかが規則的に決まってきます。
分岐経路(fork)
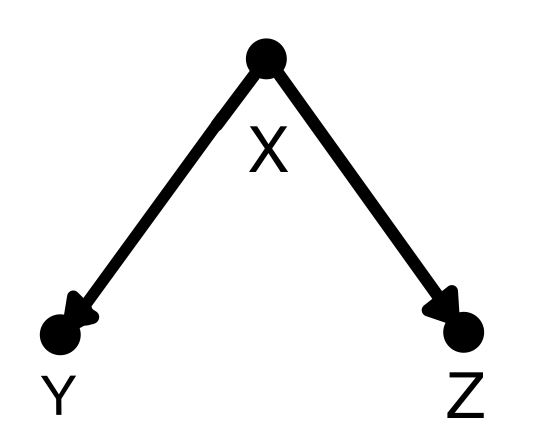
分岐経路(fork)はこのように二股に分かれる形を指します。この場合は分岐点であるXで条件付けすると分かれた先のYとZは互いに独立、条件付けしなければYとZは従属となります。
例えばある心疾患(Y)と脳疾患(Z)は直接的には関連しないものとしましょう。
どちらも運動習慣(X)があると発症しにくくなると考えてみます。グラフィカルモデルはこんな風です。
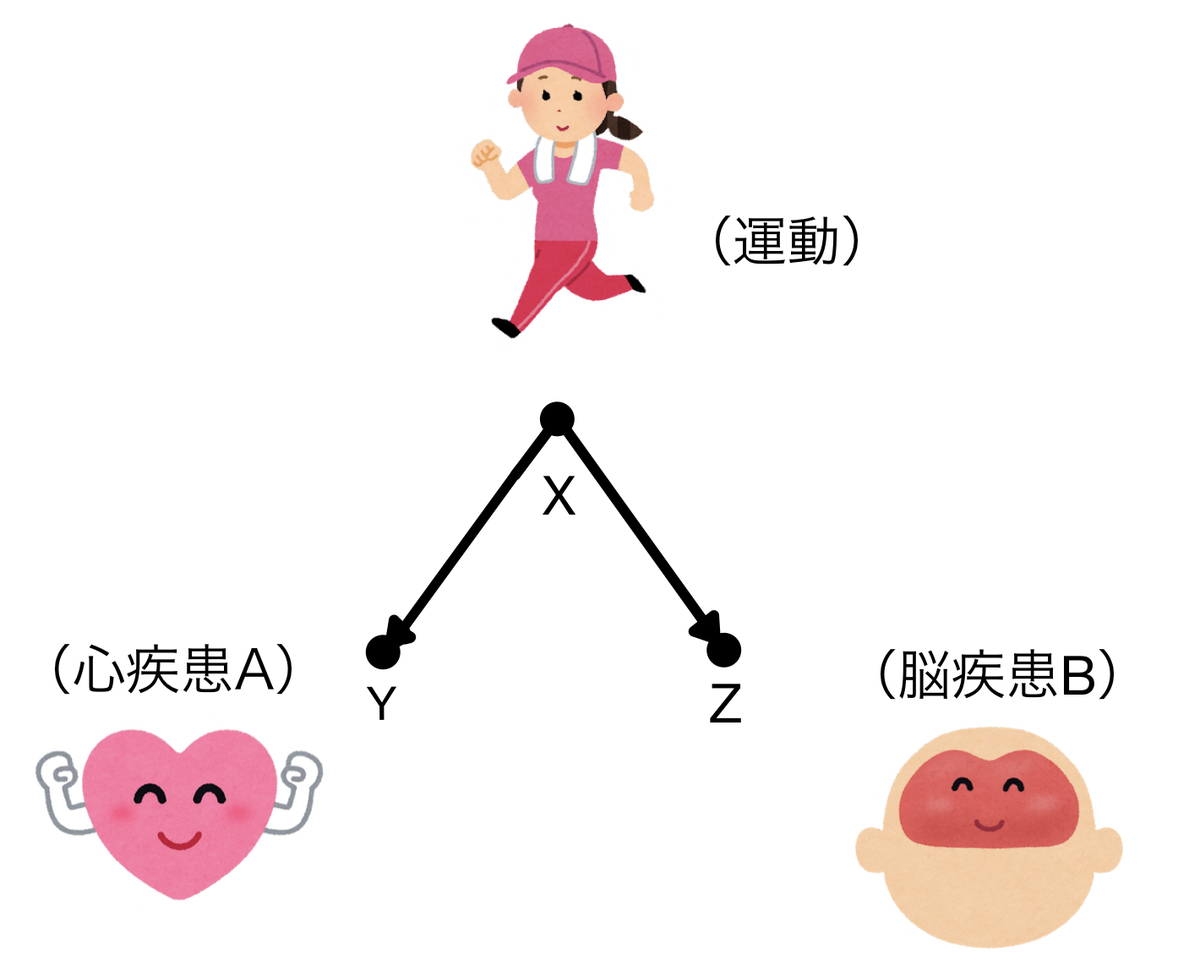
運動習慣のある人は心疾患も脳疾患も発症しにくく、運動習慣のない人は心疾患も脳疾患も発症しやすくなります。そうすると心疾患の発症しやすさが脳疾患の発症しやすさとまるで連動しているように見えます。つまり二つは従属の関係に見えるわけです。
ところが、ここで運動習慣のあるなしを固定すると、運動習慣以外にはそれぞれ独立した要因からしか影響を受けていないのため、二つの疾患は独立となります。これがfork
合流点(collider)
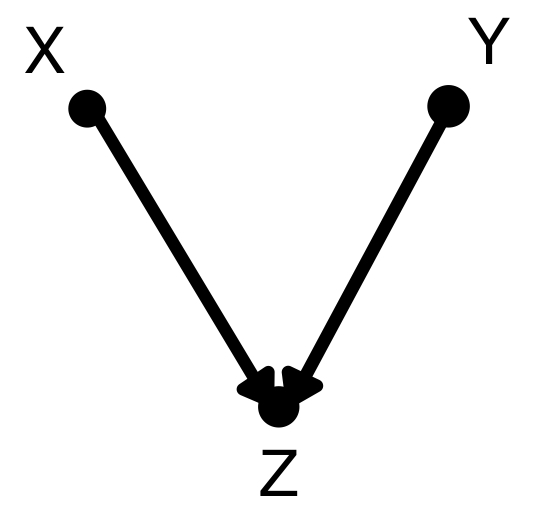
合流点(collider)はこのように二つの点が一つの点で合流します。Zで条件付けされたときXとYは従属、条件付けされないときはXとYは独立となります。forkの場合の逆ですね。
今度は例として遺伝的要因(X)と環境要因(Y)が原因となる肺疾患(Z)を考えてみましょう。
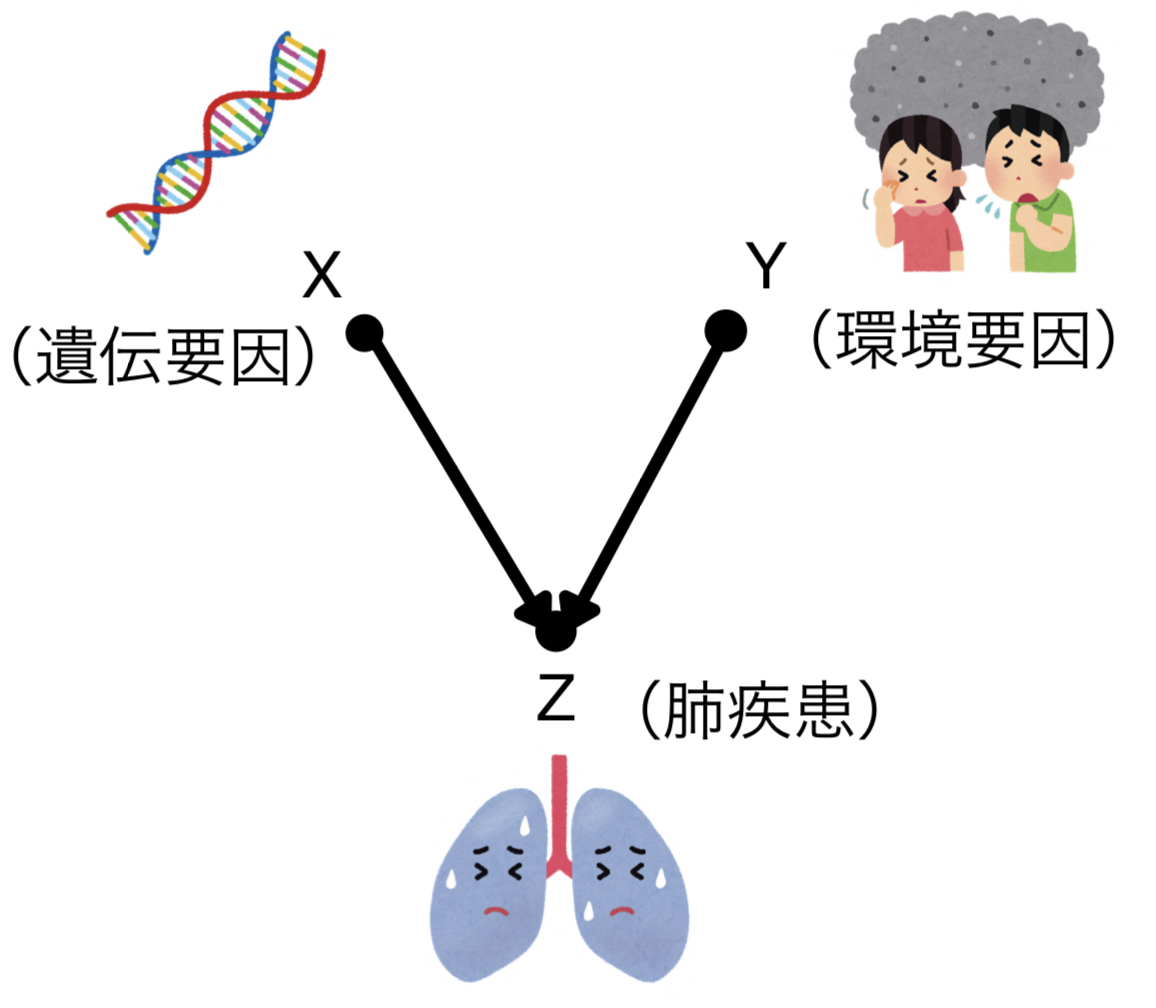
肺疾患について何の条件付けもなければ、当然ながら遺伝要因と環境要因は関係しません。不思議なことに肺疾患について条件付けをするとこの二つが従属となるのです。なぜでしょうか。
肺疾患がある人に限って考えてみたとき、例えば遺伝要因があまりなかったとします。そうすると必然的にもう一つの原因である環境要因の影響は大きいはずです。つまり、遺伝要因が小さくなることによって環境要因は大きくなってしまうわけです。従属の関係にあることがわかります。
逆もまた然りですので、以上のことから合流点について条件付けするとその原因同士は従属となります。
d-分離(d-separation)
これらの原則を用いると複雑なグラフであっても、2つのノードが独立であるかどうかを判断することができます。
あるノードの集合Zの条件が与えられた下でX,Yの二つのノードの独立となるならば「Zが与えられた下でX,Yはd-分離(d-separation)とされている」あるいは「Zによりブロックされている」と言われます。なお、d-分離のdはdirectionalを意味しているようです。
本書では従属性を水の流れのように例えて、あるノードとノードの間の道pがZによりブロックされると従属性が流れず、それぞれは独立となる、というように説明されています。
具体的な例がないとわかりづらいのでみてみましょう。
例えば下記のようなグラフィカルモデルを考えてみます。
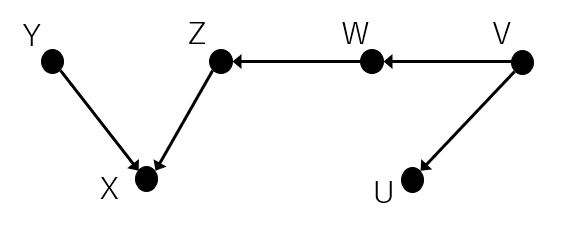
ある程度複雑な構造をしてますね。
この時YとUの関係はどうなっているでしょうか。それぞれ部分に分けてみていきます。
①Y、X、Zの関係は上記のcolliderに当てはまるため条件付けがなければYとZは互いに独立です。
②Z、W、Vは上記のchainなので条件付けがなければZとVは従属です。
③W、V、Uは上記のforkなので条件付けがなければWとUは従属です。
何も条件付けがない場合、①からYとZが独立であるため、従属性の流れはそこでブロックされます。よって、YとUはそれぞれ独立となります。逆にXのみ条件付きであれば、そこを従属性が流れるためYとUは従属となります。
ところが、Xに加えてWが条件付きとなるとどうでしょう。
そうなるとWによって従属性はブロックされます。よって、YとUは独立となります。
このように何を条件付けしたら何が周辺独立となるかが簡単に判断できることはDAGの利点となっています。
さて、ここまで読んできて紹介したモデルは簡単な例が多いです。
・疾患はそんなに単純な要因だけじゃないのではないか
・介入試験とかはどう考えれば良いのか
と思うわけですが、そこについては次の3章の内容となってくるので引き続き読み進めていきます。
Judea Pearlの入門統計学的因果推論を読んでみよう①
興味があってJudea Pearlの『入門統計学的因果推論』を昨年から読んでいるのですが、読んでいるだけだとイマイチ頭に入らないので、読んだ内容を大まかにまとめてみたいと思います。
どこかで専門的に学んでいるわけではないので誤りがあったら申し訳ありません。備忘録のようなものですが、同じように読み進めたい方の参考になれば幸いです。
第1章「序論:統計モデルと因果モデル」の内容から進めてみたいと思います。
目次:
DAGとは?
統計学的因果推論といえばDAGという用語をよく見かけます。医学界新聞でも『因果推論レクチャー』という連載が昨年から始まっていました。
因果推論で医学研究を身近で素敵なものに! | 2021年 | 記事一覧 | 医学界新聞 | 医学書院
因果推論にDAGを活用する | 2021年 | 記事一覧 | 医学界新聞 | 医学書院
第3回でDAGが紹介されています。で、そもそもDAGってなんでしょうか。
大雑把にいえばDAGは点と点を矢印で繋いで因果関係を表現したもので、たとえば最も単純なもので言えば、こんな感じです。

Xがアスピリンの使用、Yが心血管疾患の発症とすると、YはX(アスピリンの使用の有無)によって影響を受けます。これを点と矢印で端的に表現したものというわけです。
で、それがなんなの?という話になるわけですが、こうして一般化した図にすることでそれぞれの因果関係が整理しやすくなり、研究をする際にどの変数を調整するべきなのか非常に明確になります。詳細な利点は第1章の後半および第2章「グラフィカルモデルの応用」で語られることになります。
ちなみにDAGはDirected Acyclic Graphの略で、グラフ理論と呼ばれる数学の理論の中の一つです。Wikipedia, 下記サイトなどをみると何となく雰囲気がわかります。
この辺は全く知らなかったのですが、本を読み進めるときには用語に慣れておく必要があります。2章以降もグラフ理論の用語として使われるものがあるので、整理しておきます。
グラフ理論の用語
点/辺
グラフは基本的に点(ノード、node)と辺(エッジ、edge)で形成されています。
地下鉄の路線図なんかがイメージとしてわかりやすいのではないでしょうか。それぞれの点(駅)が辺で繋がれています。
有向/無向
各辺に矢印がついており向きが決まっているグラフを有向(directed)、そうでないただの線で繋がれたグラフを無向(undirected)と言います。
道(パス)
たとえばX、Y、Zの3つの要素を考えた時、下図のように繋がっていればXからZへの道(パス、path)があると言えます。

特に矢印がついていて有向である場合は有向道と呼ばれます。
巡回/非巡回
あるノードから道を辿っていって、元のノードに戻るグラフを巡回的(cyclic)グラフと言います。下図のようなイメージです。

そうでなければ非巡回的グラフです。
親/子, 先祖/子孫
有向グラフの場合に、あるノードから矢印を逆方向にたどった先にあるノードをそのノードの親(parent)と言います。逆に矢印の方向にたどった先にあるノードは子(child)です。
Yから見た場合、上の図で言えばXはYの親であり、ZはYの子です。
また、さらに多く矢印をたどった先にあるノードについては先祖(ancestor)あるいは子孫(descendant)と呼ばれます。
この図で言えばWはYの先祖ですし、TはYの子孫ですね。
さて、ここまでの用語を使えばDirected acyclic graphというのは、「有向の」「非巡回的」グラフということになります。
構造的因果モデル(SCM)とは?
因果関係を記述して扱うためのモデルとして本書では構造的因果モデル(SCM: Structual Causal Model)を用いています。
SCMというのは因果関係を外生変数の集合Uと内生変数の集合V、モデル内の変数で他の内生変数を表すための関数の集合fから成ります。
なお、先ほどの用語を交えて説明すると
外生変数=モデルの外部に存在し、モデル内の他の変数の子孫ではない
内生変数=モデルの内部に存在し、モデル内の他の変数の子孫である
というものになります。
こういってもわかりづらいので本書中の例を用いてみます。
たとえばある処置X(たとえば治療薬)と処置後の喘息患者の肺機能Yの関係を考えてみます。
通常XとYは関連があると考えられます。
冒頭の図と同じで

です。
ここで大気汚染の度合いZを考えると、ZもYに影響を与えることが想定されます。
つまり

です。
このとき、Zは外生変数、XとYは内生変数と言えます。
なぜなら大気汚染の度合い(Z)というのはどう考えたって喘息患者の肺機能(Y)や処置(X)に影響を受けるはずがないからです。
つまり、Zはどの他の変数の子孫でもありません。よって、外生変数です。
逆にXやYについてはどうでしょうか。
Yは少なくともXの子孫であるため内生変数と言えます。Xは、たとえばこれが観察研究であればもともとの呼吸機能や発作の回数、あるいはきちんと処置を受けるかどうかに影響する社会的なステータスなどなどによって影響を受けるかもしれません。そうなると他の変数の子孫となるため内生変数と考えられます。
さらに内生変数に関しては上述したように関数の集合fでそれぞれの関係が表されます。
たとえば
といった具合です。
構造的因果モデルでは“因果“をこの関数に用いられているかどうかで定義します。つまり、今回の例でいけば、Yを表す関数にXとZが使われているため、Yの直接原因はXとZである、と結論します。
SCMとDAGの関連とDAGの利点
先ほどのDAGとの関連性ですが、SCMで表した関係性を視覚的にわかりやすく表現したのがDAGということができます。
DAG以外のグラフ(あるいはグラフィカルモデル)でも表現することはできると思うのですが、本書で扱われているのはDAGになります。
完全な情報をもった式であるSCMをわざわざDAGとして描く利点としては大きく二つ挙げられています。
1つは直観的に関係性がわかりやすいこと。パッとみて何が何の原因なのか、関係性をすぐに読み取ることができます。
もう1つの利点としては、逐次的因数分解(Recursive Factorization)を使って同時分布を計算回数少なく簡単に算出できるということが挙げられています。
XがYの原因となる場合(つまりDAGでいうところのX→Y)、条件付き確率を用いると以下のようにして同時分布の計算ができたのでした。
これがX,Y,Zの3変数となった場合、同時分布をなんの情報も無しに、ただ計算しようとすると、X,Y,Zのそれぞれがとりうる値について全ての組み合わせとその頻度から多量の計算をしないといけません。
ですが、X,Y,Zが例えば以下のようなDAGで表せる場合

逐次的因数分解の法則を用いれば
と表すことができます。
考える必要のある確率がP(X=x), P(Y=y|X=x), P(Z=z|Y=y)の3つに制限されるため計算量が少なく済むわけです。
一般化すると
P(子|親)を掛け合わせれば良いということになるので
(入門統計学的因果推論p.40より引用)
と言えます。
なお、は変数
の親の変数の値を示しています。
大まかにはここまでが1章の内容(後は確率分布や条件付き分布などの基本的な話)になりまして、続いての2章ではDAGの色々なパターンや応用について述べられていきます。
次の記事はこちら
Judea Pearlの入門統計学的因果推論を読んでみよう②
参考文献:
『構造的因果モデルについて On the Structual Causal Model』黒木学
https://www.jstage.jst.go.jp/article/jjb/32/2/32_119/_pdf/-char/ja
【弱める、衰弱させる】impair/debilitate/weaken の違い【医学論文の英語表現】
「弱める」「衰弱させる」といった意味で用いられるimpair/ debilitate/ weakenについてまとめていこうと思います。
目次:
単語の意味と共起表現
・impair
to spoil something or make it weaker so that it is less effective
原義からして、もともとあった何かを弱めたり台無しにしてしまうという意味合いがあります。
共起表現でよくみられる目的語としてindependence, functioning, ability, mobility, visionなどがあり、いろいろな能力がダメになってしまうという形で使われやすいことがわかります。
特に神経内科領域では名詞形でcognitive impairmentやimpaired consciousness(いわゆる意識減損)あたりの表現を見かけることがあります。やはりいずれも元々ある何らかの能力が弱められるといった印象があります。
・debilitate
to make someone or something physically weak
他の単語との違いで際立つのはphysicallyというところでしょうか。体と直接的に関連するので共起表現も病気と関連するものが多いです。
debilitating stroke, symptoms, disease, problem, headache, illness, conditionなどですね。debilitating strokeと言われても日本語にどうも訳しにくいのですが、ing形で名詞を修飾する形は確かによく見かけます。
・weaken
to (cause to) become less strong, powerful, determined, or effective
人というよりもうちょっと大きな現象に使われることも多いのか、共起表現にはstorm, hurricaneといった自然・環境やdollar, yen, economyといった経済の単語が並びます。weakened by injury/diseaseなんていうのもありますが、あまり医学論文の場面では見られないように思います。
(Cambridge Dictionary | English Dictionary, Translations & Thesaurus
単語の原義はこちらから引用)
(SKELL共起表現はこちらを参照)
医学論文を含めた用例
・impair
・debilitate
Generalised myasthenia gravis is a rare, chronic, autoimmune disease that causes debilitating and potentially lifethreatening muscle weakness affecting ocular motility, swallowing, speech, mobility, and respiratory function, which can significantly impair independence and quality of life.
(Lancet Neurol 2021; 20: 526–36)
今回勉強の題材としていたのは重症筋無力症における新規薬エフガルチギモドの論文です。一文の中に上記の二つの単語が並んでいます。
debilitatingはmuscle weaknessを修飾しており、肉体的に衰弱させるような病気であることを述べています。
一方、impairはindependence and quality of lifeを目的語としています。上で述べたように能力や状態を”損なう”という意味合いで少し違いを感じさせますね。
またimpairは下記の文でも使われています。
These actions lead to reduced density of functional acetylcholine receptors and damage to the neuromuscular junction, resulting in impaired neuromuscular transmission.
【通常、普通】commonly/ normally/ generally/ usuallyの違い【医学論文の英語表現】
専門医試験も無事終わりましたので、ぼちぼちと英語の勉強をまた始めてます。まとまって学ぶところがあれば、たまに記事書いて勉強の糧としようと思います。
今回は「通常は、普通は」の意味で使われる副詞たちです。
目次:
単語の意味と共起表現
いずれも副詞ですが、形容詞形にも注目すると意味の違いがわかりやすいです。
・commonly
The same in a lot of places or for a lot of people
原義を見ると日本語でいう「普遍的」が近いようにも思いますが、原義にPeopleとあるように人を主体にした感じが強いですね。
Skellでcommonをみますとdisease, problem, infection, symptom, patternなどの単語が並んでいます。多くの人がなりうるという意味で人に関連した単語の形容詞として使われることが多いように思います。
動詞としてはuse, refer, call, know, find, see, associateなど知覚や知識に関連した単語が多く使われます。
・normally
If something happens normally, it happens in the usualor expected way
予想された通り、という意味での「通常は」という感じですね。また数学的な用語にも 使われうるので、「正常値」という意味合いで使われることがあります。
例えばnormalが修飾する名詞をSkellで見てみるとlevel, temperature, pressureなどの数値化できるものが並ぶのが、他との違いと言えます。
また修飾される動詞としてexpectなんかは原義に忠実な感じでしょうか。wear, eatなどの普段の生活習慣に関わる単語も見られます。
・generally
considering the whole of someone or something, and not just a particular part of him, her, or it:
「大部分が」という意味で使われますが、暗にそうでない部分もあること示される感じがありますね。
修飾される動詞としてbelieve, speak, recognize, agreeなど人の意見や信念に対する単語が多く見られる点が他と少し異なる点です。
・usually
normal; happening, done, or used most often:
頻度を示すという点が特徴となっています。
Cambridge Dictionary | English Dictionary, Translations & Thesaurus
(単語の原義はこちらから引用)
「普通」を表す Generally・Usually・Normally の違い・正しい意味・使い方、を例文を使って解説。 | フクサキENGLISH
(こちらも参考にしました)
医学論文を含めた用例
・commonly
SFN commonly refers to somatic neuropathy alone and the overlap with the term ‘painful neuropathy’ is accepted.
(Brain (2008), 131, 1912^1925)
ある用語が「多くの人や場所で」 こういう意味で使われています、という意味で使われています。用語+refer toは多く見られますね。
Side-effects are rare, with mild headache, nausea, and diarrhoea the most commonly reported.
(Lancet Neurol 2015; 14: 1023–36)
but the sixth nerve was commonly involved (four patients) as well.
(NEUROLOGY 2004;62:686–694)
報告の「頻度が多い」という意味でいずれも使われています。意味合いとしてはusuallyでもいいような気もしますが、COCAで見てみると、usuallyはブログ・雑誌などで幅広く使用されるのに対して、commonlyは圧倒的に学術関連での使用が多いです。この文章で見てもやっぱりcommonlyの方がしっくりくるように思います。
・normally
normally distributedの形で「正規分布する」という意味で使われることが、手持ちの論文を見ても、もっとも多かったのですが、それ以外にも使われてはいます。
Furthermore, epidemiologic studies suggest that diets low in sodium and high in potassium blunt the rise in blood pressure that normally occurs with age.
(Curr Hypertens Rep. 2001;3(5):373.)
「普通の場合は」という意味合いですね。この例ではcommonlyとほとんど変わらない意味であるように思います。
ちなみにここで出てくる"blunt"という単語は「鈍い」「味が薄い」という意味でよく使われる形容詞ですが、他動詞としても使われ、この文では「上昇を鈍らせる」という意味で使われています。
・generally
It is now generally accepted that earlier intervention (<5 years after onset) provides a better chance of improvement following liver transplantation
(Ikeda SI, Nakazato M, Ando Y, Sobue G. Familial transthyretin-type amyloid polyneuropathy in Japan: Clinical and genetic heterogeneity. Neurology. 2002.)
「一般的には肝移植で改善が見込まれるけれども、、、」とこの後の文章では肝移植に伴う思わぬ症状について述べられています。
上述したように「大部分はこうだけど、、、一部では」というところで使われている例ですね。
・usually
Sensory disturbance usually showed a crossed (ipsilateral face and contralateral body) or unilateral (contralateral face and body) pattern.
(Stroke. 2004 Mar;35(3):694–9.)
症状の頻度を述べる上で使われています。
aspiration is usually considered a marker for severe dysphagia
(Kumar S, Doughty C, Doros G, Selim M, Lahoti S, Gokhale S, et al. Recovery of swallowing after dysphagic stroke: An analysis of prognostic factors. J Stroke Cerebrovasc Dis. 2014)
こちらはむしろ「通常は」の意味合いに近いですね。
いずれの単語もほとんど似た意味で用いられて置換可能な時もありますが、場合によっては「頻度(usually)」「集合(generally)」「正規性(normally)」などの概念用いられており変換しづらいものもありますね。