脳内ライブラリアン

脳内ライブラリアン

医療、統計、哲学、育児・教育、音楽など、学んだことを深めて還元するために。

MENU

現代数理統計学の基礎　3章　問9

統計

ポアソン分布に従う確率変数Xがλ→∞のときに\frac{X-\lambda}{\sqrt\lambda}=Zが標準正規分布に収束することを証明する問題ですね。

 

2017年の統計検定1級の問3の最後で全く同じ問題が出ています。

お馴染みのテイラー展開を活用して解いていきます。

 

〜はどのような分布になるかか、という問題を解く際には、一つは変数変換、平方変換、確率積分変換などをして解く方法と、モーメント母関数を利用して解く方法がありますが、今回はモーメント母関数を使っていきます。

 

まずポアソン分布のモーメント母関数は

M_X(t)=exp[\lambda(e^t-1)]

でした。

 

よって確率変数Zのモーメント母関数は

M_Z(t)=E[e^tZ]\\=E[e^{\frac{X-\lambda}{\sqrt\lambda}t}]\\=e^{-\lambda t}exp[\lambda(e^t-1)]

となります。

 

続いて対数をとってキュムラント母関数にしてテイラー展開をしていきます。

logM_Z(t)=-\sqrt\lambda t+\lambda(e^{\frac{t}{\sqrt\lambda}}-1)\\=-\sqrt\lambda t-\lambda+\lambda+\sqrt\lambda t+\frac{1}{2}t^2+\frac{1}{3\lambda}t^3+...\\=\frac{t^2}{2}+\frac{1}{3\lambda}t^3+...

 

ここで2項目以降はλ→∞のとき全て0になるので

logM_Z(t)=\frac{t^2}{2}

となり、標準正規分布のモーメント母関数と一致します。

 

基本的なやり方は二項分布が正規分布に近似されるド・モアブル＝ラプラスの定理とも同じですね。以下の記事で一度解いています。

medibook.hatenablog.com 

どちらも重要な問題なので、 1級の数理統計ではまた出るかもしれません。

【統計応用・医薬生物学】Simonの2段階デザインについてわかりやすく【統計検定1級対策】

医学 統計

2017年の統計応用問3で出ていた問題が、サイモンの2段階デザイン（Simon's two-stage design）と呼ばれる、早期中止を含めた2段階のランダム化比較試験デザインでした。

 

抗がん剤の第2相試験で使われたりしているようですが、神経内科領域ではどうにも馴染みがありません。ネット上にもあまりわかりやすい記事がなかったので、一度まとめてみます。

 

目次：

 

Simonの2段階デザインとは？

具体的にどのような試験デザインになるかをまず文章で書いてみます。

①薬剤の真の奏功率を\piとします

②帰無仮説として、臨床的に無意味な奏功率を想定し\pi=\pi_0とします。また、対立仮説として臨床的に有効な奏功率を想定し、\pi=\pi_1とします。

③まず1ステージ目ではn_1人の被験者に薬剤を投与します。ここで、r_1+1名以上で有効であれば次のステージに進みます。この時点でr_1名以下にしか効果がなければ、試験は早期中止です。

④2ステージ目ではさらにn_2人の被験者に薬剤を投与します。これで全て合わせてr名以上で有効であれば、有効性が示すことができた、とします。それに満たない場合は無効と判断します。

 

図で表すとこんな感じですね。

f:id:medibook:20210324055041j:plain

 


このデザインで何がわかるかというと、αエラーとβエラーの数値を設定すれば、ここでそれぞれ文字でおいたn_1,n_2といった被験者数の内、最も少ないものを算出することができるという優れものなんですね。要はサンプルサイズの設計です。

 

被験者数の確保はランダム化比較試験において大変な問題なので、こうして目安となる数字が割り出せるのはありがたい話なわけです。

 

具体的な数式の背景

過去問に出ていたのは、Simonの2段階デザインが実際どのような数学的背景で動いているかという話。そのまま全部導出しろ、というわけではなく、小問の誘導に沿ってやっていけばなんとかできる形となっています、、、が、初見でこの誘導に沿ったとしても絶対間違えると思うんですよね。

 

というわけで簡単に流れを見ていきます。

①αエラーを起こす確率を調べる

②βエラーを起こす確率を調べる

③必要な被験者の期待値を求める（最適法 optimal design）

 

まずその前に出てくる文字の設定を確認します。

n_1 ステージ1の被験者数

n_2 ステージ2の被験者数

\pi_0 帰無仮説下の奏効率

\pi_1 対立仮説下の奏効率

r_1 ステージ1で無効と判断される人数（これ以下で無効）

r 全部のステージを総合して無効と判断される人数

x_1 ステージ1で有効であった被験者数（確率変数）

x_2 ステージ2で有効であった被験者数（確率変数）

 

では順番にみていきます。

①αエラーを起こす確率を調べる

αエラーが起きるのは、帰無仮説下（本当は治療が無効）において誤って有効と判断する確率なので、それを求めます。

 

それぞれのステージで有効となる被験者数の確率変数は確率πとなる二項分布に従うことが分かります。

 

有効となる被験者をｘ、確率をπ、被験者の総数をｎとしてb(x; π, n)という記号を用いて表すこととします。

 

するとαエラーは、ステージ1で有効と判断され、かつステージ2も有効と判断される確率なので

P(X_1\gt r_1かつX_2\gt r-X_1)\\=\sum_{x_1=r_1+1}^{n_1}b(x_1; \pi_0, n_1)・\sum_{x_2=r-x_1+1}^{n_2}b(x_2; \pi_0, n_2)

となります。

 

②βエラーを起こす確率を調べる

βエラーが起きる確率というのは、対立仮説下（本当は治療が有効）において無効と判断してしまう確率なので、こっちの方が少し複雑です。

 

なぜなら、早期中止になる場合と早期中止にはならなかったけれど、2ステージ目で中止になる場合の2パターンを考えないといけないからですね。

 

まず早期中止になる確率は①と同様に二項分布を用いて以下で表されます。

 

P(X_1\leq r_1)=\sum_{x_1=0}^{r_1}b(x_1; \pi_1, n_1)

 

 続いて 1ステージ目は有効と判断されたけれど、2ステージ目では無効と判断される確率は以下になります。

 

P(X_1\gt r_1かつX_2\leq r-x_1)=\sum_{x_1=r_1+1}^{min(n_1, r)}b(x_1; \pi_1, n_1)\sum_{x_2=0}^{r-x_1}b(x_2, \pi_1, n_2)

 

補足ですが、n_1よりもrが大きい場合と小さい場合が考えられるので最初のシグマはmin(n_1, r)となっています。

 

rの方が小さい場合、すでに 1ステージ目で有効と判断されかねないので、そのギリギリまでいくということですね。

 

ということでそれぞれを足し合わせたものがβエラーを起こす確率になります。

 

\sum_{x_1=0}^{r_1}b(x_1; \pi_1, n_1)+\sum_{x_1=r_1+1}^{min(n_1, r)}b(x_1; \pi_1, n_1)\sum_{x_2=0}^{r-x_1}b(x_2, \pi_1, n_2)

 

③必要な被験者の期待値を求める

①、②においてαエラーとβエラーを起こす確率を求めることができました。これを使って、n_1, n_2, r_1, rがどのような組み合わせであれば、αエラーとβエラーの想定値を満たすかがチェックできます。よくあるのはαエラー5％、βエラー20％（＝検出力80％）というものでしょうか。

 

条件を満たす組み合わせの中で、被験者の期待値が最小となるものを探します。

 

被験者の期待値ENは

EN=n_1-\{1-\sum_{x_1=0}^{r_1}b(x_1; \pi_0, n_1)\}・n_2

となります。

 

2ステージ目に進めるのは早期中止とならない場合なので、2ステージ目の被験者数に早期中止とならない確率を掛ければ、上の式で算出できますね。

 

こうして得られたn_1, n_2名の被験者を用いれば、サンプルサイズをうまく推定することができるわけです。

 

これがSimonの最適法（optimal design）と呼ばれています。

 

補足

この他に、αエラーとβエラーの条件を満たす組み合わせのうち、nが最小になるものの中で、先程と同様に被験者数の期待値が最小となるものを使う方法がSimonのMinimax法(Minimax design)と呼ばれます。

 

また、他にもたくさん2段階デザインはありまして

Gehan法： 1ステージ目で効果が全く期待できない時に早期中止

Fleming法： 1ステージ目で有効もしくは無効の時に早期中止

後はベイズを使った方法などなど多数あるみたいですが、統計検定に出しやすそうな程よい難易度のものはSimonの2段階デザインかな、と思うので、今後は出ないような気もします（汗

 

 

参考文献：

Simon R. Optimal two-stage designs for phase II clinical trials. Control Clin Trials. 1989 Mar;10(1):1-10. doi: 10.1016/0197-2456(89)90015-9. PMID: 2702835.

pubmed.ncbi.nlm.nih.gov

Simonの元文献です。

 

https://www.sas.com/content/dam/SAS/ja_jp/doc/event/sas-user-groups/usergroups10-a-07.pdf

ネット上に落ちてましたがスライドの図の説明が大変わかりやすいです。 

 

http://www.st.nanzan-u.ac.jp/info/gr-thesis/ms/2006/matsuda/03mm082.pdf

文章での補足程度に。

マルティン・ハイデガーの『存在と時間』に入門してみる⑥

哲学・経済学・心理学

久しく離れていましたが、そろそろとりあえず読み終えていきたいハイデガーの話をまた書いていきます。

 

前回までは現存在について重要な部分を成す気遣いと内存在が「気分」「了解」「語り」で構成され、さらにそれが本来的なものと非本来的なものに分けられることを書きました。

 

そこで本来的かつ全体的な現存在を捉えるためにはどうすればいいのか。そこで出てくるのが、今回の「死」と「不安」の話です。ハイデガーの「死」の考察は有名なのでここだけみても面白いかもしれません。

 

目次：

 

 

前回までの記事はこちら↓

マルティン・ハイデガーの『存在と時間』に入門してみる⑤

マルティン・ハイデガーの『存在と時間』に入門してみる④

マルティン・ハイデガーの『存在と時間』に入門してみる③

マルティン・ハイデガーの『存在と時間』に入門してみる②

マルティン・ハイデガーの『存在と時間』に入門してみる①

 

 

ハイデガーの「死」の捉え方

ハイデガーの哲学は「死の哲学」とも言われるくらい、このあたりの点は有名なところだと思います。まず、死の本質的な特徴を以下のように説明しています。

すなわち、現存在の終末としての死とは、現存在のひとごとでない、係累のない、確実な、しかもそれなりに無規定な、追い越すことのできない可能性である。（『存在と時間　下』p.76-77）

 

①ひとごとでない、②係累のない、③確実、④無規定、⑤追い越すことができない、と5つの特徴が出て来たのでそれぞれ簡単にみてみます。

 

①ひとごとでない

死の交換不能性とも言えますが、死ぬという行為は代わりに行うことはできません。「何かの任務のために」誰かの身代わりになって死ぬということはできても、その人の死はまたいつかやってくるわけで、代わりに受け入れるわけではありません。

 

②係累のない

今まで「気遣い」という形で周りと関連をもってきた現存在ですが、死ぬことでその関連は全て解かれてしまいます。

 

③確実

言うまでもなくどんな人間も確実にいつかは死ぬわけですが、この確実性も本当には理解されていないことをハイデガーは指摘します。「いつかは死ぬ」と言うけれど、それがいつでも差し迫っていることを分かっていないと主張します。

 

④無規定性

死は確実に起きるものでありながら、いつ起きるかは基本的にわかりません。これは医療に従事していると確かに感じますが、若いほどその可能性は低いとはいっても、予想だにしないタイミングで死がやってくることはあります。

 

⑤追い越すことができない

気遣いという形で自分に対して、色々選択をしていける可能性を常にもつ現存在ですが、死より先には可能性はありません。これ以上は追い越すことができないわけです。

 

我々が日常的に死を扱う際は、この死の本質からは逃げてしまっていることを述べます。

 

例えば、死は無規定で確実なものですが、「人はいつかは死ぬ」と言いながら「今日すぐにではないだろう」と思っているわけです。また、死は係累のないもので追い越すことができないものですが、死者をまるで今もどこかで生きているかのように扱ってみたり（きっと〜はあの世で〜しているんだろう）しています。

 

これは耐え難い死の重みに対して自分たちに鎮静をかけているものだと指摘します。

 

死に直面した時に、出てくる「気分」が「不安」であり、普段はこの「不安」から逃亡することで非本来的な生き方をしています。ハイデガーはこの「不安」という気分に重点を置いて説明しているので次は「不安」がなぜ重要なのかみてみます。

 

なぜ「不安」を重要視するのか

気分というのは前回の記事で挙げたようなハイデガー独特の術語です。

マルティン・ハイデガーの『存在と時間』に入門してみる⑤ - 脳内ライブラリアン

 

自然発生してくるようなもので、現象学的には底板であり、これ以上元には辿れない現象でした。また、気分には被投性があり、自分ではどうにもできないもの、とされていました。

 

では、不安はどのような気分なのでしょうか。ここで、ハイデガーは「恐れ」と「不安」を対比して例に出し、説明しています。

 

まず「恐れ」は対象があるもので、何かに対する恐れであるため、世界内存在の存在者のような具体的なものに対する気分です。例えば、川にいって溺れるのが怖い、だとか親に怒られるのが怖いだとかですね。

 

これに対して「不安」は対象がないことが特徴です。先程挙げた「死」がまさにそうですが、死は無規定なものでいつどのようにくるか分からず、またその後は何の可能性も無くなってしまうので、恐れのように対象がありません。

 

では何がそう不安なのかというとハイデガーは次のように述べています。

 

不安がそれを案じて不安を覚えるところのものは、世界＝内＝存在そのものである。不安のなかでは、環境的な用に具わっているものごと、一般に内世界的存在者は、崩れ落ちてしまう。「世界」も、またほかの人びとの共同現存在も、もはやなにものも提供することができなくなる。こうして不安は頽落しつつ「世界」と公開的な既成解釈からおのれを了解する可能性を、現存在から奪い去る。（『存在と時間　上』p.395-396）

 

不安の対象は世界内存在全てであるということを端的に述べています。 

 

そのため、不安という気分において、人は「頽落しつつ、既成解釈からおのれを了解する可能性」（＝非本来的な生き方）ができなくなると言っているわけです。これによって本来的な生き方が浮き彫りにされることを示しています。

 

本来的な生き方に結びつくが故に、不安をここまで重要視しているわけですね。

 

死の不安を受け入れるとどうなるか

上述した死の特徴と、不安の重要性を合わせるとどうなるでしょうか。

 

まず、不安を頽落せず（誤魔化さず）受け入れることで、本来的な生き方へ結びつくことができます。さらに死は「追い越せない」という特徴をもつため、現存在の可能性としてはそれ以上に後の点はありません。

 

よって、死の不安を受け入れることでそれ以上先のない現存在全体について本来的な生き方ができるであろうことを述べています。

 

このことをハイデガーは「先駆」してあらかじめ死を捉えて、受け入れる「＝覚悟する」と述べて、先駆的覚悟性という術語を作り出しています。

 

もう術語のあまりの多さに疲れてきますが、、、。この先駆的覚悟性は本来的な生き方をする上で重要なものですが、具体的にどうすればいいのかはあまり述べられていません。

 

これまでも割とそうでしたが、「先駆的覚悟性は〜ではない」という否定が多いのですが、肯定的な内容はあまり触れられません。先駆的覚悟性があることで、現存在は自己だけのことを考えるのでなく、むしろ自分だけのことは消滅して、周りの共存在のことを考えるようになるようです。

 

確かに、死期が間近にせまって死を受け入れた人にこうした傾向を見出すことができることもあると思います。

 

参考文献：

 

 

 

現代数理統計学の基礎　5章　問6

統計

マルコフの不等式を使った問題をやってみます。

まずは（1）から。

 

標準正規分布に従うZに対して

P(|Z|\geq t)\leq\frac{2}{t}\phi(t)

を証明します。

 

P(|Z|\geq t)\leq\frac{1}{t}E[Z| |Z|\geq t]\\=\frac{2}{t}\int_t^\infty z\phi(z)dz\\=\frac{2}{t}[-\frac{1}{\sqrt{2\pi}}exp(-\frac{z^2}{2})]_t^\infty\\=\frac{2}{t}\phi(t)

 

補足すると

マルコフの不等式はXを非負の確率変数として

P(X\geq c)\leq\frac{E[X]}{c}

と表されます。また

P(X\geq c)\leq\frac{E[X]|X\geq c}{c}\leq\frac{E[X]}{c}

とも言えるので、上記の1つ目の式変形ができます。

 

また2つ目の式変形はzが標準正規分布に従うため、対称性があるので成り立ちます。あとは実際にzを入れ込んで変形していくだけですね。

 

続いて（2）。

 

e^{-at}M_X(t)=e^{-at}E[e^{tx}]\\\geq P(e^{tX}\geq e^{ta})\\=P(X\geq a)

不等号のところでマルコフの不等式を使っています。

自動開閉式ゴミ箱Zitaを買ってみた話

雑記

4月の共働きに向けて家具・家電の新調が進む我が家ですが、ゴミ箱も自動開閉式のものを購入しました。

 

これがまた楽で良いです。

 

今までは複数のゴミ箱から45L入りのゴミ袋にまとめてたんですが、子供も増えるに従って食べ残しやら食後のゴミがどうにも増えてくるため、すぐゴミ箱がいっぱいになります。

 

ゴミ箱がいっぱいになるとゴミの日まで45Lゴミ袋に入れて置いておくんですが、0歳児がイジったり、3歳児がゴミ漁ってきたり（！？）、、、。

 

おまけに生ゴミ用のゴミ箱は開けるたびに臭いし（一応大部分はビニール袋に閉じ込めて捨てているんですが）。

 

この辺の不満はスッキリ解消されましたね。

 

購入の際に検討したところ何やら色々種類はあったのですが、蓋が縦開き式よりも横開き式の方が臭いが漏れにくいという話があったのでその中で探しました。

 

比較的有名なのは「Zita（さくらドーム）」と「賢いゴミ箱（JOBSON）」というメーカーのもの。微妙に形状が異なりまして、賢いゴミ箱の方が横長で、Zitaの方が正円に近かったです。家の置き場所も考えてZitaを選択しました。

 

良い点と悪い点を羅列していきます。

 

良い点

大容量でしっかり入る

45Lの容量があり、ゴミ袋全体に結構しっかり入ります。袋を閉めるために若干の余裕はありますが、ちょうど良いくらいだと思います。ゴミ出しが圧倒的に楽になりました。

 

生ゴミの臭いが軽減された

明らかに以前のゴミ箱より臭いは軽減されてます。全く臭わないとまでは、流石にいかないですが、それでも料理のゴミを捨てる際の不快感はかなりなくなりました。

 

センサーの感度が良い

センサーがしっかり反応してくれるので、捨てたいときに「反応しなくて開かないよチクショウ」ってことはあまりありません。爪切ったりする時とかも手が近くにあればちゃんと開いた状態を維持できます。また、センサーの反応する距離もお好みで調整できるようです。

 

 

 

悪い点

大きいゴミは入らない

これは当然なので仕方ないんですけれど、開口部以上のデカいものは入りません。なので、大きいゴミがある際は袋を出して最後に閉めるときに追加するほかありません。大きめの型紙なんかは無理やり折り曲げて捨てるしかないですね。全部まとめて捨てられる点が便利すぎて、むしろそこが気になってしまうという程度の話ですが、、、。

 

センサーの感度が良すぎる

先程の良い点と裏表の関係ですけども、センサーの感度が良すぎて近くを歩くとパカパカ反応してしまいます。反応距離の調整や向きを変えればある程度は解決できます。電池の消耗が進まないか心配になります。

 

 

パカパカ開くのが楽しいので、子どもにやたらと開閉されて遊ばれないか心配してましたが、流石に繰り返すと飽きるのか最初のうちだけでした（笑）あとはきちんとゴミ箱として使ってくれており、むしろ楽しいからか積極的にゴミを捨ててくれるので嬉しい限りです。

 

ちなみに、ゴミ箱の開閉の動画はこんな感じです。

 

 

Zitaに関しては現在も予約注文となっており、今回届いたのも1月ごろに注文したものです。（2021.3月現在、5月に配送予定）これだけ待った分のバイアスがかかってるかもしれんですが、それでも待った甲斐がありましたね。

 

子ども2人を抱えての4月からの共働きは戦々恐々としておりますが、この調子で頑張って備えていきたいと思います。

 

変数変換・平方変換・確率積分変換【統計検定1級対策】

統計

統計検定1級で頻出なテーマである確率密度関数の変数変換、平方変換、確率積分変換についてまとめてみようと思います。

 

目次：

 

変数変換

まずは変数変換から。

確率密度関数f_X(x)に従う確率変数Xに対してg(X)=Yとしたときに、Yが従う確率密度関数f_Y(y)を求める方法です。ここで、g(X)は単調増加関数とします。

 

いつも思い出す時に変換の式をちょくちょく混乱するのですが、分布関数の定義そのものから導き出すことを覚えておくと、自分で導出することで確認ができます。

 

F_Y(y)=P(Y\leq y)=P(g(X)\leq y)

ここがスタートですね。

 

次にこれを積分の式まで持ち込みます。

P(g(X)\leq y)=P\{X\in(x|g(x)\leq y)\}\\=P\{X\in(x| x\leq g^{-1}(y))\}\\=\int_{-\infty}^{g^{-1}(y)}f_X(x)dx

 

 よって

f_Y(y)=\frac{d}{dy}F_Y(y)\\=\frac{d}{dy}\int_{-\infty}^{g^{-1}(y)}f_X(x)dx\\=\frac{d}{dy}F_X(g^{-1}(y))\\=\frac{d}{dy}g^{-1}(y)f_X(g^{-1}(y))\\=\frac{1}{g'(g^{-1}(y))}f_X(g^{-1}(y))

となります。

 

g(X)が単調減少関数の場合も同様になりますので、公式としてまとめる場合

f_Y(y)=\frac{1}{|g'(g^{-1}(y)|)}f_X(g^{-1}(y))

と言えます。

 

平方変換

続いて平方変換です。

Y=X^2のような変換をする場合になります。

 

変数変換と基本的には同様の形式をたどります。

F_Y(y)=P(Y\leq y)\\=P(X^2\leq y)\\=P(X\in x|x^2\leq y)\\=P(X\in x|-\sqrt y\leq x\leq\sqrt y)\\=\int_{-\sqrt y}^{\sqrt y}f_X(x)dx

よって、

f_Y(y)=\frac{d}{dy}\int_{-\sqrt y}^{\sqrt y}f_X(x)dx\\=\frac{1}{2\sqrt y}\{f_X(-\sqrt y)+f_X(\sqrt y)\}

となります。

 

確率積分変換

統計応用医薬生物学の2017年の問１でこれを使った問題が出題されています。

 

確率積分変換は変数変換の特殊な例に当てはまりますが基本的にやることは一緒です。ある確率分布関数F_X(x)=Yと置換した時、Yは区間[0,1]の一様分布に従うというものです。

 

確率分布関数は0〜1の範囲に当てはまり（0\leq y\leq1）、また単調増加関数です。 

 

上述の変数変換の式に従えば

f_Y(y)=\frac{1}{f_X(F^{-1}_X(y))}f_X(F^{-1}_X(y))\\=1

となります。

 

過去問にも出ていましたが乱数形成にも使われる方法です。

一様分布に従うYの値を生成して、分布関数の逆関数さえ分かれば

F^{-1}_X(y)=X

とすることで任意の確率分布に従う数を生成することができます。

 

参考文献：

『現代数理統計学の基礎』

 

現代数理統計学の基礎　5章　問5

統計

統計応用もやりつつ、時々統計数理のほうも解いていっています。

今回は5章の問5。

 

順序統計量と平方変換の両方を使う良い問題です。

 

まずZ=min(X, Y)なのですが、これをどう表現するか。

解答例と同様に、順序統計量としてみて、一番小さい値と考えます。

順序統計量については以前一度記事を書いたので分からない人はどうぞ。

 

medibook.hatenablog.com

 

これに従うとZの確率密度関数は、標準正規分布の確率密度関数を\phi(z)、確率分布関数を\Phi(z)としたとき

f_Z(z)=\frac{2!}{1!1!}\{\phi(z)\}\{1-\Phi(z)\}

となります。

 

さて求めたいのはZ^2でしたので、ここから平方変換をします。

Z^2=Yとすると

f_Y(y)=\frac{1}{2\sqrt y}\{f_Z(\sqrt y)+f_Z(-\sqrt y)\}

となります。

 

先ほどのｚの確率密度関数を代入すると

f_Y(y)=\frac{2}{2\sqrt y}\{\phi(\sqrt y)(1-\Phi(\sqrt y))+\phi(-\sqrt y)(1-\Phi(-\sqrt y))\\=\frac{\phi(\sqrt y)}{\sqrt y}\{1-\Phi(\sqrt y)+1-\Phi(-\sqrt y)\}\\=\frac{\phi(\sqrt y)}{\sqrt y}

 

最後の方の式変形ですが、まず正規分布が左右対称であることより

\phi(\sqrt y)=\phi(-\sqrt y)

となります。

 

次に1-\Phi(\sqrt y)+1-\Phi(-\sqrt y)=1ですが、適当に描いた図でみるとこんな感じですね。

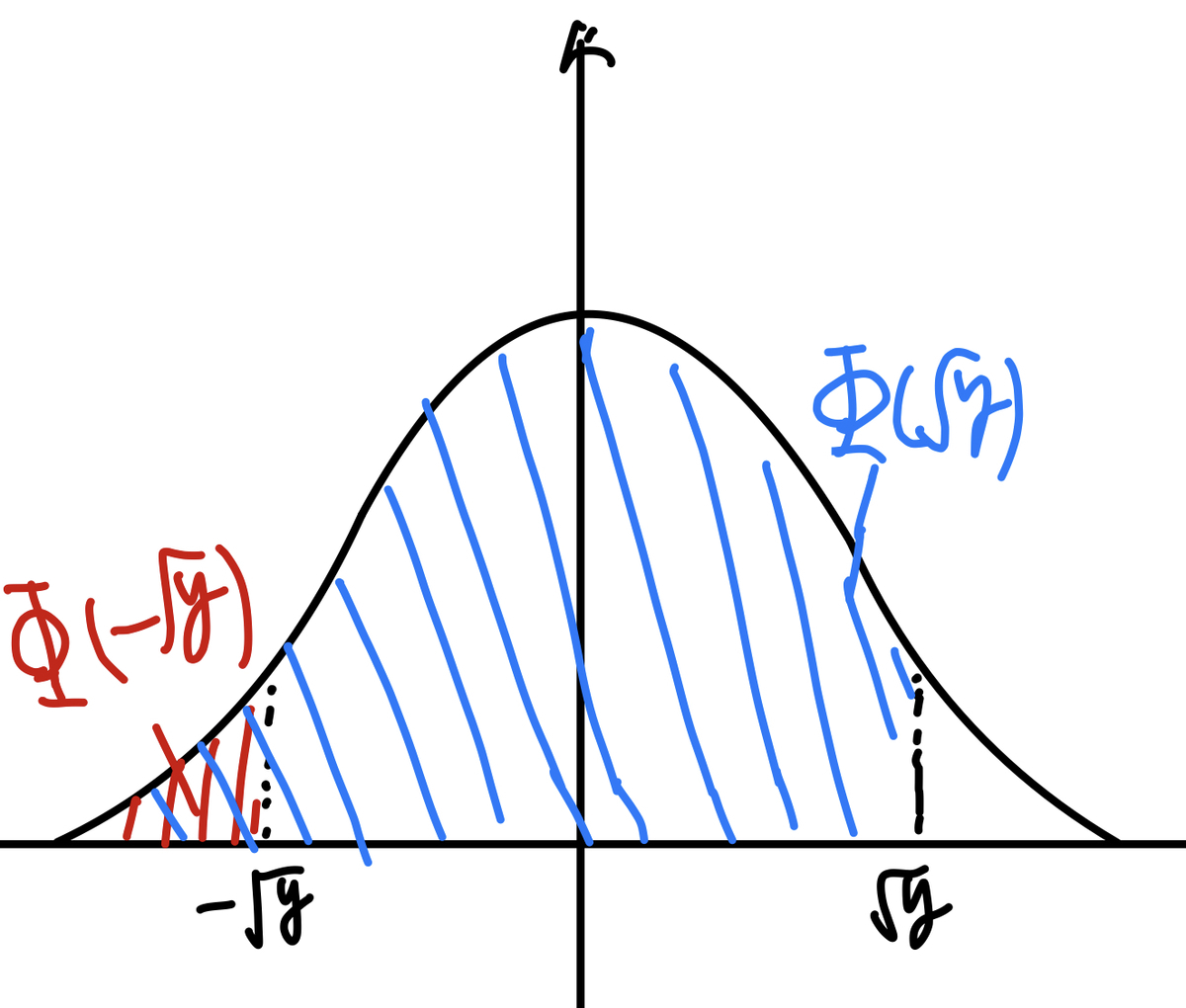
f:id:medibook:20210310062535j:plain

左右対称なので、赤と青のところを足すと１になるのが分かります。

 

かくして求められた

f_Y(y)=\frac{\phi(\sqrt y)}{\sqrt y}ですが、あとはΦのところに正規分布の式を代入すれば自由度１のカイ二乗分布に一致することが分かります。