『現代数理統計学の基礎』 解答・解説まとめ
統計検定受験が来年になってしまったので、またぼちぼち『現代数理統計学の基礎』の問題を解いていこうと思ってます。
解いた問題の解説・解答ページはここに追加していく予定です。
昔解いたものであるほど内容がショボいのもあると思います。自力で解くには問題集が難しい上に、解説も結構略されているものが多いので、「解説を読んでも答えへ行き着く方法が全然分からなかった」そんな独学者の方の参考に少しでもなれば幸いです。式よりも言葉を多めにしているつもりです。
コメント欄に気になる問題の要望・質問頂ければ時間があるときにやりますので、良ければぜひどうぞ。自分の勉強にもなるので。
(最終更新2021.10.29)
統計学検定1級対策の記事・お役立ちサイト・参考書などはこちらにまとめました。
統計検定1級の出題範囲と過去の記事・お役立ちサイト・参考書をまとめてみた【統計検定1級対策】
第2章
第3章
第4章
第5章
第6章
第7章
自動音声入力を使って英語のpodcastのtranscriptを作成する方法+主要ジャーナルのpodcast紹介
進みたい大学院や論文を書く関係でいよいよ英語の必要性が高まってきたので、勉強法や医学英語についての記事も書こうかなと思います。
今日はネットで発見して、「知っておいて良かった」と思えたpodcastのスクリプトの作り方とおまけに臨床系主要ジャーナルのpodcastをお伝えします。
目次:
Googleドキュメントを使ったpodcastのtranscript作成方法
英語のpodcastってリスニングの勉強にすごく役立ちますよね。内容も多種多様なので自分の学びたいことに合わせたpodcastが大抵1つ2つはあるんじゃないかと思います。
ただ、問題なのは内容を文字に起こした原稿(=transcript)がないものも多いことです。聞き取れなかった箇所の単語がどうしてもわからない・・・。そうなるとリスニング力の向上の障壁となります。
そこで、音声入力機能を活かしたtranscriptの作成方法を紹介します。(ちなみに、Windows10の場合です)
①Googleドキュメントを開く
Google版のwordファイルみたいなやつです。グーグルアカウントがあれば利用することができます。
②transcriptに書き起こしたいpodcastの音声ファイルを準備する
書き起こしたスクリプトが欲しいpodcastの音声ファイルをダウンロードしておきます。たいていは配信元のサイトからダウンロードできるようになっていると思います。
③マイクの設定を「サウンドミキサー」に変える
1.画面右下のスピーカーアイコンを右クリックします

2.出てきたサウンドの画面下からサウンドコントロールパネルへと移動します

3.コントロールパネルの上方のタブで録音を選びます
4.サウンドミキサーと言う項目があれば大抵「無効」になっていると思いますので、「プロパティ」から入って、「有効」に変えます
こうすることで、パソコン内で再生した音声を直接的に音声入力に導くことができます。(マイクを通してだと外部の音がノイズとなるため)
④Googleドキュメントで音声入力を行う
先ほど開いたgoogleドキュメントの「ツール」タブに音声入力の項目があります。

ここを押した後、transcriptを作りたいpodcastをWindows Media Playerなどで再生します。すると、、、

このように凄い勢いで大量の音声が書き起こされていきます。
読み込みの時間があったりすると若干の遅れが生じたり、聞き間違いも多少あることと、ピリオドや改行をしてくれないのが難点ですが、それでもないよりはかなり良いと思います。8-9割ぐらいは正答している印象です。
ぜひ、英語学習にお役立てください。
臨床系主要ジャーナルのpodcast
4大ジャーナルと言われるジャーナルのpodcastを紹介します。
臨床系の主要ジャーナルのpodcast達です。Lancetはなぜかリンクが見つかりませんでしたが、あります。
JAMAやLancetは各専門科ごとに分かれたものもあるので、例えば神経内科であれば"lancet neurology podcast"などで検索していただけると見つかります。
NEJMとJAMAは雑誌全体の研究と内容の紹介になるので、ざっと新しい記事が何かを知ることができます。概要をざっと紹介するもののほうが、比較的ゆっくり聞き取りやすく読んでくれるので、日本人にはありがたいです。
対して、LancetとBMJはざっとした概要の紹介ではなく、各論文やテーマごとに解説、専門家へのインタビューなどを行う形なので、インタビューは音質の悪さとスピードが相まって非常に聞き取りにくいです。これが聞き取れればリスニング能力は十分だと思いますが、、、自分はまだまだなのでtranscriptに起こして、精進しようと思います。
超幾何分布でおさえておきたいポイントとフィッシャーの直接確率検定【統計検定1級対策】
さて、今回は確率分布の話で見直していたら忘れかけていた超幾何分布の話を書こうと思います。
目次:
超幾何分布とは?
超幾何分布は確率論で良く出てくる「箱から2種類のボールを取り出す問題」で出てくるボールの個数が従う分布です。例えばこんなシチュエーションです。
「ある箱には赤いボールがM個、白いボールがN-M個入っています。そこから全部でn個のボールを戻さずに取り出すとき、そのなかにある赤いボールの個数をx個とします。」
このxが従うのが超幾何分布となります。
式としては通常の確率論と同じで、分母に全てのボールの組み合わせである、分子に
を置いて
となります。
これが何の役に立つかというと、臨床医学的には2×2分割表がこの状況に類似されます。
例えば、アスピリンの内服によって、脳梗塞の発症が抑えられるかどうかをみたランダム化試験があるとしましょう。すると2×2分割表は以下のように作られます。

この数値が帰無仮説<脳梗塞の発症とアスピリンあり/なしが関連しない>のもとでは、超幾何分布に従うので、超幾何分布の式から事象が起きる確率を計算することができます。
アスピリンあり/なしを先ほど例でいう赤いボールと白いボール、脳梗塞を発症した人を取り出したボールの数と考えれば超幾何分布に従うことは分かると思います。
これを使った応用例がフィッシャーの直接確率検定(後述)です。
また、ログランク検定もこの確率分布を使っています。以前に記事で書きました。
超幾何分布の総和が1となることの証明
さて次に、超幾何分布が確率分布となること(総和が1となること)を確認しておきたいと思います。
これは二項定理を使うのですが、この証明と等式が分かっていれば、平均・分散の証明にも役立つので、ここがおさえておきたいポイントです。
まず超幾何分布において総和が1になるというのはこの式になります。
変形すると
この式が期待値・分散の導出においても役立ちます。
この式の証明は二項定理を用いて行います。
まずある実数a,bを用いて
であり、二項定理を使うと
(二項定理について分からない場合は↓を参照)
となります。
ここで、展開した際に同じ係数を持つ者同士を比較するのがポイントとなります。
の係数をもつものを左右で比較してみましょう。
すると(左辺)においては
となります。
次に(右辺)では前半のかたまりと後半のかたまりを掛け合わせて同じを創り出します。
と分解すればよいので、係数は
となります。
さらに、を創り出せる組み合わせはx=0~Mまであるので係数は
となります。
以上から
を示すことができました。
超幾何分布の平均・分散の導出の概略
上記の式を用いれば平均と分散は導出していくことができます。
細かい変形まで書くのが少し面倒なので(すみません)、概略までにとどめます。
まず平均は定義に沿って
です。
手順を言葉にすると
①使わないをくくり出す
②和の記号のx=0をx=1に変える(後で活きてきます)
→結局はx=0だと0になるので同じ
③combinationを階乗に分解して、xをその中に組み込む
④あとはひたすら整理してcombinationに戻す
⑤x-1=yなどに置き換えて、ずらす(②の意味が出てきます)
⑥(総和の式の変形)を使う
と言う感じです。
③~④を端折りますが
となります。
分散についても全く同様の過程で導くことができます。
を始めとしてあとは変形していくのみです。
分散の式を使って導出します。
フィッシャーの直接確率検定(Fisher's exact test)について
超幾何分布を応用した例としてフィッシャーの直接確率検定(またはフィッシャーの正確確率検定) を紹介します。
先ほど出てきた2×2分割表を利用するような場合に使われる検定方法です。
上述したように、2×2分割表で表のような数値になる確率は超幾何分布に従うことが分かります。ただし、これはその2×2の要素が互いに関連がないという帰無仮説のもとで従うことになります。ボールの例でいえば「赤いボール」と「白いボール」が出てくる確率は完全にランダムで、どちらが出やすいというのはないはずです。
ただ、超幾何分布で単純に出せるのは「その表のようなデータが出る確率のみ」ですので、帰無仮説がどうかを仮説検定するものではありません。
そこで、「得られた表のようなデータ」よりもさらに極端(確率的に起こりにくい)なデータの出る確率を全て足し合わせていきます。先ほどのアスピリンと脳梗塞の表で再度みてみましょう。

これよりも極端なデータというのは「アスピリンあり」が「脳梗塞あり」にさらに含まれないようになるデータのことを指します。2×2分割表の周辺和(下図赤枠)を固定とみなして、そのような極端なデータの確率を足し合わせます。

この足し合わせた確率が有意水準以下であれば、帰無仮説を棄却できます。
グラフでイメージするとこのような感じです。

確率の総和である赤が有意水準の確率と比べて大きいかどうかで仮説検定をします。
カイ二乗検定との違い
よく言われるのは、2×2分割表の際に同じ帰無仮説に対して使われるχ二乗検定との違いです。今回は細かい原理には触れませんが、内容は簡単に書いておこうと思います。
カイ二乗検定はあくまで、上に示した直接確率検定と違い、カイ二乗分布への近似を用いています。直接確率検定は”直接”の名前の通り、そのまま計算していますので、こちらのほうがより”正確”です。「集計表に10以下の数があればフィッシャーの直接確率検定」だなんて言われたりしますが、別に計算可能であれば、こっちのほうが確実なので、10以上でも良いと思われます。
こちらのサイトの生物統計基礎セミナーの<仮説検定2>の講座でもそのように言われています。登録すれば無料で講義を沢山みれるので、おすすめです。
さらにカイ二乗検定の場合は、もともと離散型確率変数(整数しかとらない)である2×2分割表の内容を、連続型確率変数であるカイ二乗分布に変えている関係で、「イェーツの補正」と呼ばれる補正を掛けなければいけません。もとの数に近い形を保てるという意味ではやはりフィッシャーの直接確率検定のほうが良いでしょう。
かつては手計算で出していたので、数が多くなったらカイ二乗検定と言われる名残があるのだと思いますが、今やパソコンの計算能力は上がってますので可能ならフィッシャーの直接確率検定で間違いはないかと思っています。
参考文献:
今年の統計検定1級が中止になっていた・・・
そろそろ申し込もうかと思って公式ホームページみてみたところ。
2020年11月の統計検定試験の中止について(新型コロナウイルス感染症への対策(確定))|統計検定:Japan Statistical Society Certificate
中止になってました・・・。
1級の次回は2021年11月・・・。
まあやむをえないですかね、、、人数減らして実施、みたいなことも書いてあったので期待していたのですけれど。モチベーションをどこに持っていったものか。
統計数理と応用の2つがあり、今回は数理だけ受けようと思っていたので、来年に応用と両方受かるようにまた勉強していきたいと思います。
読書が好きな人にこそ勧めたい『難解な本を読む技術』
「分かったつもり」になっているけど、実はよくわからない本や概念ってないでしょうか。
本を沢山読むことの良さを語った本や、読書の意味/記憶術/速読の方法なんて本はたくさんありますが、難しい本を理解する方法について説いた本は少ないです。
先日買って個人的にはクリーンヒットした読書術の本を紹介します。こちらです。
読書が好きな人、読書が少しずつ好きになってきた人、難解な文献を読む必要がある人にぜひオススメしたいです。
目次:
既存の読書術本の問題点
以前に読書術の本を紹介する記事を一度書きました。
読書術について書かれた本をまとめてみる① - 脳内ライブラリアン
結局のところお勧めしたのは佐藤優著『読書の技法』でしたが、なぜこの本を一番勧めたかったかというと、その理由のひとつとして、熟読の仕方をきちんと説明しているということにあります。
狭く深い専門的な知識の掘り下げ方は入口を浅くみるよりも当然難しいです。ただ、その分学ぶ価値は大きい。
以前紹介したDaigoさんの本にせよ、樺沢紫苑の本にせよ、対象者を幅広くしている分(ゆえに良く売れるのだと思いますが)知識を掘り下げる方法という点ではどうしても甘いと思うのです。どちらの方も専門的な書籍を読んでいるでしょうし、本人は難しいものも読めるのだとは思いますが、間口を広くとっている分そこの説明は薄いように感じます。
しょっちゅう出されては消えていくビジネス書なども時には大いに学ぶところがあるのですが、大きな価値を持ちうるのはもっと専門的な文献であったり、名著と言われる哲学書でもあると思うのです。そうした本をキチンと読む方法を紹介するのが今回紹介する『難解な本を読む技術』です。
自分が読みたい哲学の本を題材として書かれている本ですが、それ以外でも、文系の要素を含む専門的な分野を独学で学ぶ必要があるときには役立つと思います。
本のタイプを分類する
まずこの本では本のタイプを、①「開いている」「閉じている」、②「登山型」「ハイキング型」、③「外部参照あり」「なし」、の3点で分類します。その理由としては分かっていたほうが理解の速度が明らかに速くなるからです。
①「開いている」「閉じている」
本には筆者の自己主張が明確ではなく、読者に考えさせる「開いている本」と自己主張が明確であり、そのための論理や根拠が並べられている「閉じている本」があります。
理系の文献や論文なんかは基本的に「閉じている」と言えますし、よく売られているビジネス書も基本的には「閉じている本」が多いと思います。ただ、例えば色々な方法論を紹介して、結論は出さないような本(『~大全』とか)は「開いている本」と言えます。
「開いている本」で結論や自己主張を探し出そうとしたり、一貫した論理を紡ごうとするのは時間の無駄になります。そのことに気づくことが大事です。『~大全』みたいなのが、結論はない本だよ、っていうのは読む側にも分かりやすいのですが、初見で気づきにくくて難しいのはやはり哲学書でしょう。ミシェル・フーコーなんかは代表的な「開いている本」なようです。
②「登山型」「ハイキング型」
最初の方から論理的に根拠や知識の積み上げを行っていくのが「登山型」、いろんな要素を紹介していく形なのが「ハイキング型」です。
例を出して言えば数学の参考書や英文法の本というのは大部分が「登山型」と言えるかもしれません。前の事項が分かってないと次の章へ進んでいけません。
それに対して「ハイキング型」は章ごとに風景を楽しむような感じでどこから入っても読むことができます。事典なんかは明らかにこちらですね。通読するものではありません。
本の中である一つの章ごとに知識の積み上げが必要である、小さな山が連なっているような「登山型」というのもあるので注意が必要です。
③「外部参照あり」「なし」
これはその本の中で知識が完結しているかどうかを指します。他の本などから知識や用語の解説が必要なものは「外部参照あり」、そうでないものは「外部参照なし」となります。
細かいことを言えば「外部参照の全くない本」なんてものはないと思いますが、その人の持っている知識によって外部参照が必要なレベルは異なると思います。
例えば、「統計学」の本を読むにあたって、微分積分・確率論といった知識は先だって必要です。理系の分野は基本的に知識の積み重ねが必須なので、その意味では「外部参照あり」となります。
「哲学」においてもその分野ごとの基本的知識が要求されることは多いと思います。例えば「実存主義」のサルトルの本を読もうとしたときに、ハイデガーの使う「存在」の意味(辞書的な定義とは異なる)を、知っておかないとちんぷんかんぷんになってしまいます。
これらの分類をすることが大切なのは、本の読み方に自覚的になることです。それによって後から「本を読む」段階に入ったときに、効率に大きく影響が出てきます。
本を読む準備を進める
筆者はこの読む準備にはしっかり時間をかけて必要な本を選び抜くことをお勧めしています。「棚見」といって本屋でその分野の本の棚をざっとみて、目次を沢山みていくことで、知りたい分野の全体像を構成することを勧めています。そのうえで、読みたい本を厳選すべき、としています。
目的に沿わない本や、意味が全く理解できない本を読むことは無駄どころか余計な時間がかかる、と言うことをたびたび強調しています。ソフトウェアエンジニアの言葉を借りて「ゴミが入ればゴミが出る」とまで言っています。
これは確かに大事なことで、佐藤優『読書の技法』*1でも触れられていましたが、人が本を読める数というのはかなり限られています。月10冊ペースで本を読んだとしても、年間120冊で、30年で3600冊。これが中学校の図書館くらいと言われています。統計局の報告*2によれば、書籍の新刊点数は年間約75000冊とされていますので、人生の大部分を割いても読めるのは年間に出る書籍の20分の1以下です。
こういわれると何時間もかかるきちんとした読書をしようと思ったらよくよく選ばないといけない、と言う意味が良くわかるのではないでしょうか。
実際に本を読み進める
本書では通読→詳細読みという流れと読書ノートの作成を推奨しています。
まず、1回目に通読することで、知識の外形(全体の俯瞰図と流れ)や上で述べた本のタイプ、用語分からない箇所、難解な部分と簡単な部分などをうまく整理することができます。この際に本の目次を書き写した読書ノートを使ってメモしながら通読することで上記のポイントがうまく整理できる、としています。
通読の仕方も、本のボリュームとタイプによって少し分けており、章毎に短く区切って戻る場合と全部一気に読んでしまう場合、理解できなくなったら数ページごとに戻る場合があります。「登山型」の場合は特に短めにして戻ることを勧めています。
こうして(範囲は色々ですが)通読をしたら次に詳細読みに入ります。論理関係や用語の意味をきちんと洗いだし、読書ノートにメモしていきます。この段階で初めて本の思想を理解できるところへ入ります。
この段階で分からない部分というのは以下の問題のどれかだと、本書では指摘しています。
①用語の理解が不十分
②論理関係の把握が不十分
③問題の理解が不十分
④図にできないと理解が不十分
何度も読み直したり、「外部参照のある」本は他の書籍を読み進めるもしくはネットで調べたりすることで解決していきます。ただ、本当に難解な本は何年たってもうまく理解できないことはあり、それはザラだと言われています。
ただ、ここまでして理解できたと言える知識は、現実に使うことのできるものと十分に言うことができそうです。
雑感
著者も現代思想を専門にした本をいくつか書いており、基本的には哲学書を読むことを前提としていますが、それ以外の分野にも十分に応用が効く話です。
本書の後半では具体的な思想家の本の読み方(フーコー、ラカン、デリダなど難解なものを多く含む)と実際の読書ノートの例も載せてあるので、これも参考になります。
今まで自分もそれなりに本を読んできて、「なんとなく気になったから、とりあえず読んでみる」という段階は卒業して「現実生活に活かす読書」にスキルアップしていきたいところです。そういった方に本書は役立つと思います。
参考文献:
*1
実際の医学論文から統計を学んでみるⅡ②-イベント数/人年データをNNTに直す方法-
前回の記事からの続きで、ELDERCARE-AF studyを題材にして考えていきます。
実際の医学論文から統計を学んでみるⅡ①-ELDERCARE-AF study/ IPCW法- - 脳内ライブラリアン
臨床的に解釈のしやすいのはNumber Needed to Treat(NNT)ですが、このstudyのような生存時間解析の場合は通常の計算方法ではうまく出せません。生存時間解析においてNNTをどのように出すか、を説明します。
目次:
人年データにおけるNNTの算出方法
通常、観察期間の決まっているRCTであれば、普通の式通りに絶対リスク減少(ARR: absolute risk reduction)をまず算出し、逆数をとれば、NNTが出ます。
ARR=(コントロール群のイベント数/人)- (介入群のイベント数/人)
NNT=1/ARR
という式ですね。ちなみにこれは介入でイベントが減るということを前提にしています。
ELDERCARE-AF studyで出されているのは人年あたりのイベント数なので本来はこの式とはちょっと違います。コントロール群が6.7%/人年、介入群は2.3%/人年で合計の観察人年はそれぞれ約650人年ほどでした。これを1年のあたりのイベント数が6.7, 2.3であると仮定して、無理やり当てはめてみます。
すると、
ARR=4.4%
NNT=22.727...
となります。
結論から先に書くと人年データの場合の正しい計算方法*1は
ARR={1-exp(-コントロール群のイベント数/人年)}-{1-exp(-介入群のイベント数/人年)}
NNT=1/ARR
です。
同様にstudyの結果に当てはめると
NNT=23.771
となります。
実は結構似通った値になるわけですが(汗
発症頻度が低い場合はあまり値は変わりません(差が出る場合は後述)。*2
しかし、なぜこの2つの式の違いが出てくるのか。詳細は以下で説明していきます。
累積発症率の伸びは徐々に緩やかになる
上述の違いは累積発症率をどういう式で推定するか、によった違いに起因します。
ある人が単位時間あたりイベントを発症する確率をλ(0<λ<1)、累積発症率をF(t)(tは時間)として話を進めます。
まず最初の方法の場合。コントロール群について本来約650人年の観察期間で44人にイベントがあったというもの、を単純な割り算で1人年あたり6.7人にイベントが起きたと計算しています。つまり累積発症率をλtと推測して計算しています。F(t)=λtとおけます。
グラフだとこんな感じです。

実はここが間違いで、累積発症率は時間経過する場合、徐々に伸びが緩やかになります。
具体的な例を考えたら分かりますが、月間20%がイベントを起こす疾患を100人に対して観察していった例で考えてみると
1か月後:残り80人、累積発症率20%
2か月後:残り64人、累積発症率36%
3か月後:残り51人、累積発症率49%
4か月後:残り41人、累積発症率59%
・・・
累積発症率の伸びが緩やかになってきているのが分かります。
それを考慮したモデルが2つ目の方法になるわけです。で、なぜそこにexp(自然数)が出てくるかと言うと、数式の話に入らざるを得ません(汗。苦手でない方のみどうぞ。
ハザード関数と指数分布
2個目の計算式を出す方法も同様に単位時間あたりイベントを発症する確率をλ(0<λ<1)、累積発症率をF(t)、それを微分したものをf(t)として説明します。
2個目の計算式はある瞬間における死亡率をλと考えます。
これを式にすると
①ある時間 tまではイベントが起きていないという条件のもとで
②ある時間 tから極小の時間 t+Δの間でイベントが起こる確率
となるので、①の条件付きで②が起きる確率になります。*3
Tをイベントが起きる時間として式をたてると
となります。
補足ですが、縦棒|は条件付きの意味を表します。
また前提として変形には分布関数の知識が必要です。
です。
こちらもご参考ください。
12-1. 累積分布関数とは | 統計学の時間 | 統計WEB
先ほどの式の両辺をΔで割って、極小と考えると微分の定義を使って
となります。
最初の左辺こそが、瞬間の死亡率(ある極小の時間t~t+Δにイベントが起こり、かつそれまではイベントが起きていない確率)に他ならないのでλと等しくなります。
よって
となります。
となるので
ですから整理して
となります。
変数を時間のtに変えると
となるので、2つ目の関係式が導き出せたことが分かります。
今回はλを定数と考えて計算していますが、λがtに依存する関数として考えると一般的なハザード関数と呼ばれるものの定義になります。
二つの計算方法を並べてグラフにすると、イメージとしてはこんな感じになるので最初の方法とは違うことと、こちらの計算方法のほうが常に小さくなることが分かります。
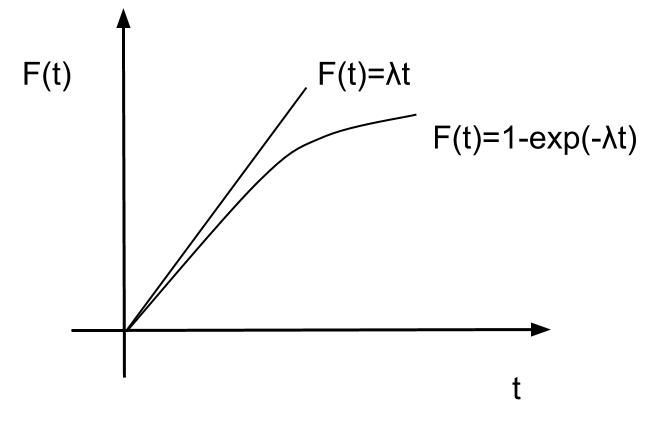
実際、二つの差をG(t)として考えると
微分して
となり、G(t)は単調増加かつ、G(0)=0なので上記のようなグラフが想定できます。
ただ、実際のところ、グラフの最初の方は差が小さいことが分かると思いますが、λが小さい場合(=発症頻度が低い場合)や時間経過が短い場合は、二つの計算方法であまり誤差は出ません。なので、最初の計算でもあまり数値に差がつかなかったわけです。
ちなみに、F(t)を微分すると
となります。これは指数分布と呼ばれる確率分布になります。λを定数として考えた場合に生存時間を示す確率分布です。
話が色々と広がってしまいましたが、今回の計算方法を応用すれば、生存時間解析データから1年あたりのNNTを算出し放題なので、ぜひ臨床研究を解釈する際にお役立てください。
(補足)果たして計算方法で差が出るのかどうか
(2020.10.09追記)
理論上はこの計算方法が良いですよ、と言う話なのですが、コメントでご指摘いただいたように、実際のところはあまり計算方法で差が出ることは多くないと思います。
差が出る例として参考文献*2に出されている例をみてみます。
それぞれ100人を1年観察した研究で、コントロール群のイベント数が80, 介入群のイベント数が40として考えます。
通常の方法で考えると
(コントロール群のイベント数/人)=0.8
(介入群のイベント数/人)=0.4
NNT=1/(0.8-0.4)=2.5
となります。
それに対して、ハザード関数の原義に忠実な計算方法で考えると(計算は省略)
NNT=4.5
となります。
こうなるとNNTに倍に近い誤差が出るので大きいように感じますが、こうしたことが起きるのは、例のようにかなり発症率が大きい場合ですね。
100人を1年観察して80%がイベントを起こすような試験ってかなり無茶苦茶です。そこまで頻度の高いかつ大事なイベントって基本的にない(重要なアウトカム=重篤なアウトカム=さすがにそこまで頻度は高くない)ので、まずここまでの差はないのでしょう。
実際の臨床試験でみられるような数%~数十%のイベント数であれば基本的にはどちらの方法でも差はあまりないと思います。手計算でできる分、通常の計算方法でも普段は十分なのでしょう。
(2021.06.28追記 医学論文の読み方関係の記事はこちらにまとめました)
参考文献:
*1Number Needed to Treat (NNT) Calculator
情報を入れれば自動で先ほどの計算式から算出をしてくれる便利なサイトです。
*2Stang A, Poole C, Bender R. Common problems related to the use of number needed to treat. J Clin Epidemiol. 2010;63(8):820-825. doi:10.1016/j.jclinepi.2009.08.006
NNTの算出について問題点を指摘している論文です。上記サイトで引用されていました。
*3『現代数理統計学の基礎』
実際の医学論文から統計を学んでみるⅡ①-ELDERCARE-AF study/ IPCW法-
前にも同じようなことやりましたが、最近読んだ論文から統計学的な手法の勉強をしたので、再確認しつつ紹介します。
論文の内容自体は、脳梗塞に対するDOACのstudyですが、日本国内のstudyで、かつ高齢者への今までにないエドキサバン低用量投与という興味深いものだったので、内容も合わせて書きます。
以前の記事はこちら。
目次:
- ELDERCARE-AF study
- そもそも打ち切り例の補完はなぜ必要か
- IPCW法(Inverse Probability of Censoring Weighting Method)とは
- IPCW法の問題点
ELDERCARE-AF study
題材にする論文はまだ8/31に出たばかりのstudyで、今までエドキサバン(リクシアナ®)が処方されなかったような高齢者に対して投与したらどうなったかというものです。
論文はこちら
Low-Dose Edoxaban in Very Elderly Patients with Atrial Fibrillation
The Edoxaban Low-Dose for EldeR CARE Atrial Fibrillation patients trialなので略してELDERCARE-AFなようです。
対象者は80歳以上かつCHADS2 score2点以上の患者群のうち、通常エドキサバンを始めとしたDOACを出さないような背景因子(以下)
・CCr15-30
・出血性疾患の既往
・体重45kg以下
・抗血小板薬を内服中
・NSAIDs継続使用中など
の人に対して処方したランダム化比較試験です。めちゃくちゃ攻めてますね・・・。
用量は当然通常の用量より低く、15mg/日という少量です。
計984名を集め、観察の中央値は466日でした。primary outcomeは脳卒中もしくは全身の塞栓性イベントです。primary safety outcomeはmajor bleedingとしています。
結果はprimary outcomeがハザード比0.34 (介入群2.3%/人年 vs コントロール群6.7%/人年, 95%CI: 0.19-0.61, p<0.01)
対してprimary safety outcomeはハザード比1.87 (介入群3.3%/人年 vs コントロール群1.8%/人年, 95%CI: 0.90-3.89)でした。
secondary safety outcomeをみると、majorでなくても治療を要したclinically relevant bleedingがまあまあ多いのは気になりますが、、それでも本来不適格な高齢者に脳梗塞予防の道を開いた点では結構興味深いのではないでしょうか。
これだけの高齢者を集めてのstudyというのが日本ならでは!という感じがあって個人的には面白かったです。当然ながら第一三共(エドキサバンのメーカー)がスポンサーには入っているのはやむなしでしょうか。
ただ、このstudyで問題となるのは高齢者が多すぎるがゆえに、途中脱落の患者(=censoring)が多いということです。そもそも脳梗塞起こさなくても他の原因で亡くなる場合があるのと、通院困難となる事例もあると思われます。各群ともに150名ほど抜けているので驚きの打ち切り率、約30%です、、、。
さて、こうした場合に役立つ方法がIPCW法(Inverse Probability of Censoring Weighting method)です。概念を紹介します。
そもそも打ち切り例の補完はなぜ必要か
IPCW法は打ち切り例(=欠測データ)を補完する方法のうちのひとつです。
そもそもなぜ打ち切り例に補完が必要かという話ですが、打ち切りが完全にランダムに存在するする場合であれば問題ありません。問題なのは、臨床試験において実際はランダムではなく、打ち切りには何らかの要因が存在することが多いことです。
例えば今回の研究の打ち切り事例を想定してみると、80歳以上の超高齢者が主体の研究なので、何らかの疾患(転倒での骨折や認知症、介護者の高齢化)で通院自体ができなくなったり、あるいは癌や心不全、肺炎などprimary outcome以外の要因で亡くなること(競合リスクcompeting riskと呼ばれます)もあり得るわけです。
これらは明らかにランダムではなく、例えば少なくとも年齢とは関連性がありそうなことがわかります。
そうなると打ち切られた例には偏りが存在するため、解析に用いている打ち切られていないデータは実際の臨床像から乖離してしまう可能性が出るわけです。そこでIPCW法を始めとした補完方法が活用されます。
では、実際にIPCW法とは何をしているものなのか。
IPCW法(Inverse Probability of Censoring Weighting Method)とは
IPCW法は「被験者が観察される確率の逆数で被験者を重み付けた解析」(文献*1より引用)とあります。これだけで分かれば良いのですが、自分の場合はさっぱりだったので、より分かりやすく砕いてみていきます。
まず、打ち切り例と非打ち切り例について先に述べたように要因がどこにあるかを調べ、関連しそうなデータ(共変量もしくは回帰分析であれば説明変数と言われるもの)を見つけ出します。
例えば今回のstudyであれば別疾患による死亡や通院できなくなる疾患発症などがあるので、年齢は少なくとも共変量となることが推測されます。(実際は分かりませんが)
そこから打ち切りになる確率を推測するモデル(数式)を作ります。流れを図にまとめるとこんな感じです。

こうして作られた打ち切りになる確率を推定するモデルを使って、非打ち切り例の打ち切りになる確率を計算します。
例えば、ある被験者Aについて打ち切りになる確率が80%だったとしましょう。

そうすると打ち切りにならない確率は1-0.8=0.2なので20%と分かります。
とすると、実際は被験者Aと同じような被験者が結構打ち切られていた(80%の確率)可能性があることが分かります。
打ち切りにならない確率の逆数をとって1/0.2=5なので、あと「4人くらい同じような被験者がいたはずだけど打ち切られた」ことが推定されます。

この分をいわば水増しして、計算するのがIPCW法です。被験者Aのデータは5倍に水増しされて、primary outcomeを算出するための計算に組み込まれます。
言葉にすると、最初に述べたように「被験者が打ち切られない確率の逆数をとって重みづけをする」ということになります。
こうして確認してみると、名前の通りで「打ち切り確率の(Probability of Censoring)逆確率(inverse)で重みづけ(weighting)をしたよ」ということですね。傾向スコアにおけるIPTW法と考え方としては似ています。
今回のstudyではそれによって打ち切り例の分も補正して解析を行っていますが、結果は変わらなかったようです。
IPCW法の問題点
想定できるだけでもいくつか挙げられます。
まず、最初の打ち切りになる確率を算出する統計モデルについて、推定がきちんとできているのかどうか。未知の交絡因子の存在や原因推定が不十分であると根底となるモデルに欠陥が起こります。
また、文献*2からの引用になりますが、IPCW法では、補正のやりすぎの問題が起こりえます。臨床現場においてコンプライアンス不良や通院の中断といった事象は実際に起こりうることです。それによって起きた打ち切り例も補正を行うとかえって過度な補正がされたことになり、生存期間やアウトカムについて実臨床的なデータとの乖離が起こりえます。
さらに競合リスクについてもこれは同様です。競合リスクによる死亡も実臨床上避けられない話なので、これを補正することは実際以上に生存期間を長く推定することにつながります。今回のstudyのように高齢者が主体であれば、なおさら影響が大きいので、効果については過剰な評価になっている可能性を考えないといけないように思います。
次回は同じ研究をネタにしてイベント数/人年データを用いたNumber Needed to Treatの算出方法について書きます。
(2021.06.28追記 医学論文の読み方関係の記事はこちらにまとめました)
参考文献:
*1嘉田 晃子, 松山 裕, 佐藤 俊哉ら著. 中止·脱落の理由を考慮した IPCW法による臨床試験データの解析. 計量生物学2002 年 23 巻 2 号 p. 81-91 J-STAGEへのリンク
*2 Howe CJ, Cole SR, Chmiel JS, Muñoz A. Limitation of inverse probability-of-censoring weights in estimating survival in the presence of strong selection bias. Am J Epidemiol. 2011;173(5):569-577. doi:10.1093/aje/kwq385 pubmedへのリンク



